Tìm nghiệm nguyên của phương trình : x2 +x=x2y-xy+y
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình x y + y 2 + x = 7 y ( 1 ) x 2 y + x = 12 ( 2 ) thì tích xy bằng:
A. 1
B. 2
C. 3
D. 4
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

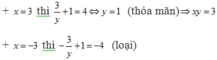

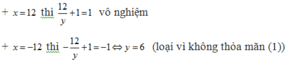
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
Tìm nghiệm nguyên của phương trình : x2 - xy +y2 = x-y
<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0
giải phương trình nghiệm nguyên: x+y+xy=x2+y2
\(x+y+xy=x^2+y^2\)
⇔ \(2xy+2x+2y=2x^2+2y^2\)
⇔ \(\left(x^2+y^2-2xy\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)=2\)
⇔ \(\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2=2\)
⇔ 
⇔ 
Các cặp số nguyên (x, y) thỏa mãn phương trình là : (0; 0); (2; 2); (0; 1); (2; 1); (1; 0);(1;2).
Nếu (x;y) là nghiệm của phương trình x 2 y − x 2 + 2 x y − x + 2 y − 1 = 0 thì tổng giá trị nhỏ nhất và giá trị lớn nhất của y là:
A. 2
B. 3
C. 3/3
D. 1
Đáp án A
y − 1 x 2 + 2 y − 1 x + 2 y − 1 = 0 1
Nếu y = 1 thì x = 1
Nếu y ≠ 1 thì để (1) có nghiệm thì
Δ = 2 y − 1 2 + 4 y − 1 2 y − 1 ≥ 0 ⇔ 2 y − 1 3 − 2 y ≥ 0 ⇔ 1 2 ≤ y ≤ 3 2
⇒ min y = 1 2 ; max y = 3 2 ⇒ min y + max y = 2
1. tìm nghiệm nguyên của phương trình:
p(x + y) = xy và p nguyên tố
2. tìm nghiệm nguyên của phương trình:
a. x + y + z + 9 = xyz
b. x + y + 1 = xyz
Tìm nghiệm nguyên của phương trình sau
x3+x2y+2xy3=x2y2+y4
tìm nghiệm nguyên của phương trình : x3 - x2y + 3x -2y - 5 = 0
Lời giải:
PT $\Leftrightarrow x^3+3x-5=x^2y+2y=y(x^2+2)$
$\Rightarrow y=\frac{x^3+3x-5}{x^2+2}$
Để $y$ nguyên thì $x^3+3x-5\vdots x^2+2$
$\Leftrightarrow x(x^2+2)+x-5\vdots x^2+2$
$\Leftrightarrow x-5\vdots x^2+2(1)$
$\Rightarrow x^2-5x\vdots x^2+2$
$\Leftrightarrow x^2+2-(5x+2)\vdots x^2+2$
$\Leftrightarrow 5x+2\vdots x^2+2(2)$
Từ $(1);(2)\Rightarrow 5(x-5)-(5x+2)\vdots x^2+2$
$\Leftrightarrow 27\vdots x^2+2$. Do $x^2+2\geq 2$ nên:
$\Rightarrow x^2+2\in\left\{3;9;27\right\}$
$\Rightarrow x^2\in\left\{1;7;25\right\}$
Do $x$ nguyên nên $x\in\left\{\pm 1; \pm 5\right\}$
Thay vào $y$ ta tìm được:
$x=-1\Rightarrow y=-3$
$x=5\Rightarrow y=5$
Tìm tất cả các giá trị của tham số m để hệ phương trình x 2 - m = y ( x + m y ) x 2 - y = x y có nghiệm
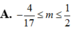
![]()
![]()
![]()
1. Tìm nghiệm nguyên của phương trình xy-x+y=4
\(xy-x+y=4\)
\(\Leftrightarrow x\left(y-1\right)+y-1=3\)
\(\Leftrightarrow\left(x+1\right)\left(y-1\right)=3\)
Kẻ bảng :
| x+1 | 1 | -1 | 3 | -3 | |
| y-1 | 3 | -3 | 1 | -1 | |
| x | 0 | -2 | 2 | -4 | |
| y | 4 | -2 | 0 | 0 | |
| KL | tm | tm | tm | tm |
Vậy ...
p/s: check lại hộ tui nhá =)))