Tìm x biết 3xy-2x+y =3

Những câu hỏi liên quan
Tìm giá trị của đa thức biết x - y = 3
x^3 - y^3 - 4xy + y^2 - 35 - 3xy(x -y) + 2x^2
Tìm x,y nguyên biết
xy+2x+y=3
3xy+x+y=6
TÌM X,Y THUỘC Z BIẾT
xy+x-2y=3
3x+5y+175
3xy+6x+y_32=0
2x+5y+3xy=8
4xy-3(x+y)=59
xy-x-y=2
TÌM X BIẾT
a)2(3x-1)(2x-1)-(2x-3)(9x-1)-3=-3
b)3xy(x+y)-(x+y)(x2+y2+2xy)+y3=27
tìm số tự nhiên x , y biết :
a) (x+5)(y-3)=15
b)3xy +2x+2y=0
tìm x y nguyên biết
3xy - 2x - 2y = 24
giúp
Lời giải:
$3xy-2x-2y=24$
$\Rightarrow (3xy-2x)-2y=24$
$\Rightarrow x(3y-2)-2y=24$
$\Rightarrow 3x(3y-2)-6y=72$
$\Rightarrow 3x(3y-2)-2(3y-2)=76$
$\Rightarrow (3x-2)(3y-2)=76$
Vì $x,y$ nguyên nên $3x-2, 3y-2$ cũng là số nguyên. Do đo $3x-2, 3y-2$ là ước của 76.
Đến đây thì đơn giản rồi. Bạn chỉ cần xét các TH khác nhau của ước của 76.
Đúng 3
Bình luận (1)
Tìm x; y thuộc Z biết 2x + y - 3xy = 10
Nói chung là ko giải dc chứ gì, thế nên mới chỉ quan tâm đến avartar
Đúng 0
Bình luận (0)
tìm số ngyên x,y biết: 3xy - 2x + 5y = 9
Lời giải:
$3xy-2x+5y=9$
$x(3y-2)+5y=9$
$3x(3y-2)+15y=27$
$3x(3y-2)+5(3y-2)=17$
$(3x+5)(3y-2)=17$
Do $x,y$ nguyên nên $3x+5, 3y-2$ cũng là số nguyên. Ta có bảng sau: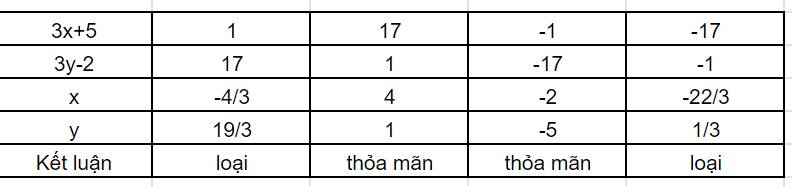
Đúng 2
Bình luận (0)
Tìm x, y biết:\(\hept{\begin{cases}x^2+y^2+xy=3\\2x^2+3xy=1+4x\end{cases}}\)
\(\hept{\begin{cases}x^2+y^2+xy=3\left(1\right)\\2x^2+3xy=1+4x\left(2\right)\end{cases}}\)
Lấy (1) + (2) ta được
\(3x^2+y^2+4xy-4-4x=0\)
\(\Leftrightarrow\left(y+x-2\right)\left(y+3x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y=2-x\\y=-2-3x\end{cases}}\)
Thế \(y=2-x\)vào (1) ta được
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow x=1\Rightarrow y=1\)
Tương tự cho trường hợp còn lại.
Đúng 0
Bình luận (0)


















