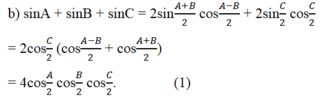Trong tam giác ABC chứng minh: sinC = sinAcosB + sinBcosA
![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)
Những câu hỏi liên quan
CM: sinC=sinAcosB+sinBcosA
\(A+B+C=180^0\Rightarrow C=180^0-\left(A+B\right)\)
\(\Rightarrow sinC=sin\left[180^0-\left(A+B\right)\right]=sin\left(A+B\right)\)
\(\Rightarrow sinC=sinA.cosB+cosA.sinB\)
Đúng 0
Bình luận (0)
CHo tam giác ABC có ba góc nhọn thỏa mãn điều kiện:
\(\frac{4}{sinB+sinC}=\frac{1}{sinB}+\frac{1}{sinC}\)
Chứng minh rằng tam giác ABC cân
Đặt \(sinB=x\) , \(sinC=y\)
Áp dụng BĐT Cauchy : \(\left(x+y\right)^2\ge4xy\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
Đẳng thức xảy ra khi x = y , hay \(sinB=sinC\Rightarrow\widehat{B}=\widehat{C}\) , suy ra tam giác ABC cân.
Đúng 0
Bình luận (0)
Chứng minh rằng trong tam giác ABC có:
a) tanB = tan( A+C)
b) sinC = sin( A +B)
c) cos A = -cos (B+C)
a: ΔABC có góc B+góc C+góc A=180 độ
=>góc B=180 độ-góc C-góc A
=>tan B=tan(A+C)
b: ΔABC có góc C+góc B+góc A=180 độ
=>góc C=180 độ-góc B-góc A
=>sin C=sin(A+B)
c: Xét ΔABC có góc A+góc B+góc C=180 độ
=>góc A=180 độ-góc B-góc C
=>cosA=-cos(B+C)
Đúng 1
Bình luận (0)
cho tam giác abc nhọn. chứng minh rằng:
sinA+sinB+sinC<2(cosA+cosB+cosC)
Cho tam giác ABC AB =c, BC =a , AC=b. Chứng minh 2SinA=SinB + SinC
Cho tam giác ABC nhon, đường cao AH. Chứng minh rằng AB×SinB=AC×SinC
Cho tam giác ABC vuông tại A . Từ trung điểm E của cạnh AC kẻ EF vuông góc với AC tại F
a) Cho BC = 20cm, sinC = 0,6. Giải tam giác ABC;
b) Chứng minh rằng : AC2 = 2CF.CB
c) Chứng minh : AF = BC.cosC
cho tam giác ABC có bán kính đường tròn ngoại tiếp bằng 1,thỏa sinA/mA+sinB/mB+sinC/mC=căn 3.chứng minh tam giác ABC đều
Giả sử A, B, C là ba góc của tam giác ABC, chứng minh rằng: sin A + sin B + sin C = 4 cos A 2 cos B 2 cos C 2