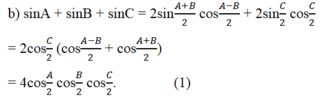Các câu hỏi tương tự
Cho A,B,C là ba góc của một tam giác. Chứng minh rằng:
\(\sin A+\sin B-\frac{\sqrt{2}}{2}\cos C\le\sqrt{2}\)
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
chứng minh rằng
a) tanx(cot\(^2\)x - 1) = cotx(1 - tan\(^2\)x)
b) tan\(^2\)x - sin\(^2\)x = tan\(^2\)x.sin\(^2\)x
c) \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}\) - cos\(^2\)x = - cos\(^4\)x
CMR: Biểu thức sau không phụ thuộc vào x: A=-sin⁴x +cos⁴x + 2sin²x B=sin⁴x + cos²x × sin²x + cos²x C= cos⁴x + cos²x × sin²x + cos²x
Đưa về tích rồi giải các phương trình sau:
a) \(\sin 2x -2.\sin x +\cos x -1=0\)
b) \(\sqrt{2} . (\sin x - 2.\cos x) = 2-\sin 2x\)
c) \(\frac{1}{\cos x} - \frac{1}{\sin x}=2\sqrt 2 .\cos(x + \frac{\pi}{4}) \)
Cho A,B,C là các góc của tam giác. Chứng minh các đẳng thức sau: a. cos(A+B)+cosC=0 b. cosA+B/2=sinC/2 c. cos(A-B)+cos(2B+C)=0
1/ Cho \(cot\alpha=\sqrt{5}\) . Tính \(C=sin^2\alpha-sin\alpha cos\alpha+cos^2\alpha\)
2/ Cho \(tan\alpha=3\) . Tính \(B=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}\)
Bài 1: Phương trình căn 2 cot x + căn 2=0 có tổng các nghiệm khi k =0 và k=1?
A.3pi/4 B.5pi/4 C.4pi/3 D.pi/2Bài 2:cho sin a=1/3,0<a<pi/2 tính sin( a-pi/4) Bài 3:cho cos a=-2/3,pi/2<a<pi tính cos ( a+pi/3)
Giúp vs bạn
Tìm \(\alpha\) biết:
a) \(\sin\alpha=0\)
b) \(\sin\alpha=1\)
c) \(\sin\alpha=-1\)
d) \(\cos\alpha=0\)
e) \(\cos\alpha=1\)
f) \(\cos\alpha=-1\)
Giải các PT sau:1. dfrac{left(2cos2x-1right)left(sin x-3right)}{sin x}0 2.dfrac{3left(sin x+cos xright)}{sin x-cos x}2+2cos x3.dfrac{3left(sin x+tan xright)}{tan x-sin x}-2cos x24. 1+sin x+cos x+sin2x+cos2x05. 2sin xleft(1+cos2xright)+sin2x1+2cos x
Đọc tiếp
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)