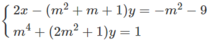
Chú ý rằng   m 2   +   m   +   1   >   0 ;   - m 2   -   9   <   0 , ∀m nên nếu x > 0, y < 0 thì phương trình thứ nhất có vế trái dương, vế phải âm. Do đó không có giá trị nào của m làm cho hệ đã cho có nghiệm thỏa mãn điều kiện x > 0, y < 0.

a) Thay m=0 vào phương trình (1), ta được:

\(x^2-2\cdot\left(0-1\right)x+0^2-3m=0\)

\(\Leftrightarrow x^2+2x=0\)

\(\Leftrightarrow x\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)

Vậy: Khi m=0 thì S={0;-2}

Lời giải:
Để pt có 2 nghiệm phân biệt thì $\Delta'=1-(m-3)>0$

$\Leftrightarrow 4-m>0\Leftrightarrow m< 4$

Áp dụng định lý Viet:

$x_1+x_2=2$

$x_1x_2=m-3$
Khi đó:
$x_1^2-(x_1+x_2)x_2+x_1x_2=-12$

$\Leftrightarrow x_1^2-x_2^2=-12$

$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$

$\Leftrightarrow 2(x_1-x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$

Kết hợp với $x_1+x_2=2$ thì $x_1=-2; x_2=4$

$m-3=x_1x_2=(-2).4=-8$

$\Leftrightarrow m=-5$ (tm)

              Bài làm :

a) Thay m=-5 vào PT ; ta được :

\(x^2-2x-8=0\)

\(\Delta'=\left(-1\right)^2-1.\left(-8\right)=9>0\)

=> PT có 2 nghiệm phân biệt :

\(\hept{\begin{cases}x_1=\frac{1+\sqrt{9}}{1}=4\\x_2=\frac{1-\sqrt{9}}{1}=-2\end{cases}}\)

b) Đk để PT có 2 nghiệm phân biệt :

\(\Delta'>0\Leftrightarrow\left(-1\right)^2-1.\left(m-3\right)=1-m+3=4-m>0\)

\(\Rightarrow m< 4\)

Khi đó ; theo hệ thức Vi-ét ; ta có :

\(\hept{\begin{cases}x_1+x_2=2\left(1\right)\\x_1x_2=m-3\end{cases}}\)

Mà : 

\(x_1=3x_2\Rightarrow x_1-3x_2=0\left(2\right)\)

Từ (1) và (2) ; ta có HPT :

\(\hept{\begin{cases}x_1+x_2=2\\x_1-3x_2=0\end{cases}}\Rightarrow\hept{\begin{cases}x_1=\frac{3}{2}\\x_2=\frac{1}{2}\end{cases}}\)

\(\Rightarrow x_1x_2=\frac{3}{4}\Rightarrow m=\frac{3}{4}+3=\frac{15}{4}\left(TMĐK\right)\)

Vậy m=15/4 thì ...

a,x\(^2\)-2x+m-3=0 (*)

thay m=-5 vào pt (*) ta đk:

x\(^2\)-2x+(-5)-3=0⇔x\(^2\)-2x-8=0

                       Δ=(-2)\(^2\)-4.1.(-8)=36>0

      ⇒pt có hai nghiệm pb

         \(x_1=\dfrac{2+\sqrt{36}}{2}=4\) , \(x_2=\dfrac{2-\sqrt{36}}{2}=-2\)

vậy pt đã cho có tập nghiệm S=\(\left\{4;-2\right\}\)

b,\(x^2-2x+m-3=0\) (*)

Δ=(-2)\(^2\)-4.1.(m-3)=4-4m+12=16-4m

⇒pt luôn có hai nghiệm pb⇔Δ>0⇔16-4m>0⇔16>4m⇔m<4

với m<4 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)

theo hệ thức Vi-ét  ta có:

\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=m-3\end{matrix}\right.\)       (1) ,(2)

\(x_1,x_2\) TM \(x_1=3x_2\) (3)

từ (1) và (3) ta đk:

\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=\dfrac{3}{2}\end{matrix}\right.\)

thay \(x_1=\dfrac{3}{2},x_2=\dfrac{1}{2}\) vào (2) ta đk:

\(\dfrac{3}{2}.\dfrac{1}{2}=m-3\Leftrightarrow3=4m-12\Leftrightarrow4m=15\Leftrightarrow m=\dfrac{15}{4}\) (TM)

vậy m=\(\dfrac{15}{4}\) thì pt (*) có hai nghiệm pb \(x_1,x_2\) TMĐK \(x_1=3x_2\)

Áp dụng hệ thức vi-ét:

\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=m-1\end{matrix}\right.\)

Ta có:

\(x_1^2+x^2_2=30\)

\(\left(x_1+x_2\right)^2-2x_1.x_2=30\)

\(4^2-2\left(m-1\right)=30\)

\(2m-2=-14\)

\(m=-6\)

Để phương trình đã cho có hai nghiệm \(x_1,x_2\) thì 

\(\Delta'>0\Leftrightarrow2^2-\left(m-1\right)=5-m>0\Leftrightarrow m< 5\)

Khi \(m< 5\) phương trình đã cho có hai nghiệm \(x_1,x_2\).

Theo định lí Viete ta có: 

\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m-1\end{matrix}\right.\)

Ta có: 

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(m-1\right)=18-2m=30\)

\(\Leftrightarrow m=-6\) (thỏa mãn) 

a, x 2 − 2 ( m + 1 ) x + m 2 + m − 1 = 0 (1)

Với m = 0, phương trình (1) trở thành:

  x 2 − 2 x − 1 = 0 Δ ' = 2  ;  x 1 , 2 = 1 ± 2

Vậy với m = 2 thì nghiệm của phương trình (1) là  x 1 , 2 = 1 ± 2

b) Δ ' = m + 2

Phương trình (1) có hai nghiệm phân biệt  ⇔ m > − 2

Áp dụng hệ thức Vi-ét, ta có:  x 1 + x 2 = 2 ( m + 1 ) x 1 x 2 = m 2 + m − 1

Do đó:

     1 x 1 + 1 x 2 = 4 ⇔ x 1 + x 2 x 1 x 2 = 4 ⇔ 2 ( m + 1 ) m 2 + m − 1 = 4 ⇔ m 2 + m − 1 ≠ 0 m + 1 = 2 ( m 2 + m − 1 ) ⇔ m 2 + m − 1 ≠ 0 2 m 2 + m − 3 = 0 ⇔ m = 1 m = − 3 2

Kết hợp với điều kiện  ⇒ m ∈ 1 ; − 3 2  là các giá trị cần tìm.

b: \(\text{Δ}=\left(2m+3\right)^2-4\left(4m+2\right)\)

\(=4m^2+12m+9-16m-8\)

\(=4m^2-4m+1=\left(2m-1\right)^2>=0\)

Do đó: Phương trình luôn có hai nghiệm

Theo đề, ta có:

\(\left\{{}\begin{matrix}2x_1-5x_2=6\\x_1+x_2=2m+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1-5x_2=6\\2x_1+2x_2=4m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x_2=-4m\\2x_1=5x_2+6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\2x_1=\dfrac{20}{7}m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\x_1=\dfrac{10}{7}m+3\end{matrix}\right.\)

Theo đề, ta có: \(x_1x_2=4m+2\)

\(\Rightarrow4m+2=\dfrac{40}{49}m^2+\dfrac{12}{7}m\)

\(\Leftrightarrow m^2\cdot\dfrac{40}{49}-\dfrac{16}{7}m-2=0\)

\(\Leftrightarrow40m^2-112m-98=0\)

\(\Leftrightarrow40m^2-140m+28m-98=0\)

=>\(20m\left(2m-7\right)+14\left(2m-7\right)=0\)

=>(2m-7)(20m+14)=0

=>m=7/2 hoặc m=-7/10

Đáp án C

Đặt f ( x ) = a x 2 + b x + c  là là hàm số đa thức nên liên tục trên .

Ta có: f ( 0 ) = c  và

f 1 3 = a 9 + b 3 + c = a + 3 b + 9 c 9 = 2 a + 6 b + 18 c 18 = ( 2 a + 6 b + 19 c ) − c 18 = − c 18

⇒ f ( 0 ) . f 1 3 < 0

KL: Phương trình a x 2 + b x + c = 0  có ít nhất một nghiệm thuộc khoảng  0 ; 1 3