giúp bài 2 b

giúp em câu b bài 1 và ý 2 câu b bài 2 ạ
bài 1: Cho a/b=c/d.CMR ac/bd=a2+c2/b2+d2
bài 2: Cho a/b=c/d.CMR a/a-b=c/c-d
bài 3: Cho a/b=b/c=c/a.CMR a=b=c
Giúp mik với.Cần lắm ai giúp đỡ với T_T
ddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddd
dddddddddddddddddddddddddddđ
qqqqqqqqqqqqqwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww
xxxxxxx
Giúp mình phần b bài 2 và bài 3
Bài 2:
\(\left|\left|x^3-4\right|+21\right|:5=5\)
\(\Leftrightarrow\left|\left|x^3-4\right|+21\right|=25\)
\(\Leftrightarrow\left|x^3-4\right|+21=25\) hay \(\left|x^3-4\right|+21=-25\)
\(\Leftrightarrow\left|x^3-4\right|=4\) hay \(\left|x^3-4\right|=-46\) (vô lí do \(\left|x^3-4\right|\ge0\forall x\))
\(\Leftrightarrow x^3-4=4\) hay \(x^3-4=-4\)
\(\Leftrightarrow x^3-8=0\) hay \(x^3=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)=0\) hay \(x=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\right)=0\) hay \(x=0\)
\(\Leftrightarrow\left(x-2\right)\left[\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\) hay \(x=0\)
\(\Leftrightarrow x=2\) hay \(x=0\) hay \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\) (vô nghiệm do \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\))
-Vậy \(S=\left\{0;2\right\}\)
Bài 3:
\(\left|\left|2x^2-2\right|+6\left|x^2-1\right|\right|=4^6:\left(2^3\right)^2\)
\(\Leftrightarrow\left|\left|2x^2-2\right|+6\left|x^2-1\right|\right|=64\)
\(\Leftrightarrow\left|2x^2-2\right|+6\left|x^2-1\right|=64\) (*) hay \(\Leftrightarrow\left|2x^2-2\right|+6\left|x^2-1\right|=-64\) (pt vô nghiệm do \(\left|2x^2-2\right|+6\left|x^2-1\right|\) luôn là số thực dương)
-Có: \(\left|2x^2-2\right|=2x^2-2\) nếu \(x\ge1\) hay \(x\le-1\).
\(\left|2x^2-2\right|=-2x^2+2\) nếu \(x\le1\) hay \(x\ge-1\).
\(6\left|x^2-1\right|=6\left(x^2-1\right)\) nếu \(x\ge1\) hay \(x\le-1\)
\(6\left|x^2-1\right|=-6\left(x^2-1\right)\) nếu \(x\le1\) hay \(x\ge-1\)
-TH1: \(x\le-1\):
(*) \(\Leftrightarrow2x^2-2+6\left(x^2-1\right)=64\)
\(\Leftrightarrow2x^2-2+6x^2-6=64\)
\(\Leftrightarrow8x^2-72=0\)
\(\Leftrightarrow x^2-9=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=3\) (loại) hay \(x=-3\) (nhận)
-TH2: \(-1\le x\le1\):
(*) \(\Leftrightarrow-2x^2 +2-6\left(x^2-1\right)=64\)
\(\Leftrightarrow-2x^2+2-6x^2 +6=64\)
\(\Leftrightarrow-8x^2-56=0\)
\(\Leftrightarrow8x^2+56=0\) (pt vô nghiệm do \(8x^2+56\ge56\forall x\))
-TH3: \(x\ge1\):
-TH1: \(x\le-1\):
(*) \(\Leftrightarrow2x^2-2+6\left(x^2-1\right)=64\)
\(\Leftrightarrow2x^2-2+6x^2-6=64\)
\(\Leftrightarrow8x^2-72=0\)
\(\Leftrightarrow x^2-9=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=3\) (nhận) hay \(x=-3\) (loại)
-Vậy \(S=\left\{3;-3\right\}\)
Bài 1: Tìm max A: A = -x^2-6x+14
Bài 2: Tìm min B: B= 4x^2+12x+30
Giúp mik với!
Bài 1 :
\(A=-x^2+6x+14\)
\(A=-x^2+6x-9+23\)
\(A=-\left(x^2-6x+9\right)+23\)
\(A=-\left(x-3\right)^2+23\)
Vì \(-\left(x-3\right)^2\le0\)
\(\Rightarrow A=-\left(x-3\right)^2+23\le23\)
\(\Rightarrow Max\left(A\right)=23\)
Bài 2 :
\(B=4x^2+12x+30\)
\(\Rightarrow B=4x^2+12x+9+21\)
\(\Rightarrow B=\left(2x+3\right)^2+21\)
Vì \(\left(2x+3\right)^2\ge0\)
\(\Rightarrow B=\left(2x+3\right)^2+21\ge21\)
\(\Rightarrow Min\left(B\right)=21\)
Giải chi tiết phần b bài 1 và phần b bài 2 giúp em với ạ
Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)
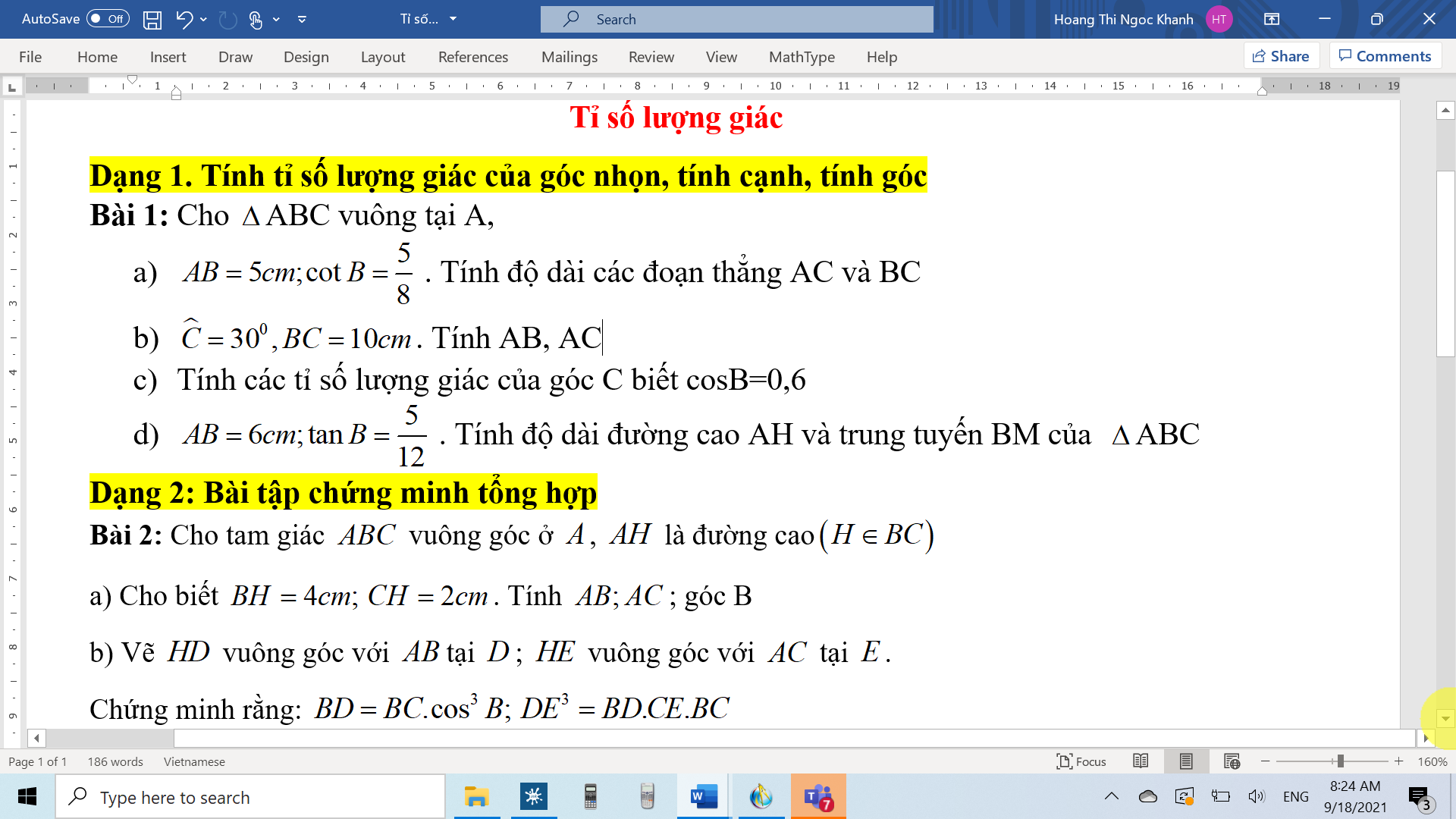
GIÚP EM CÂU C,D BÀI 1,CÂU B,D BÀI 2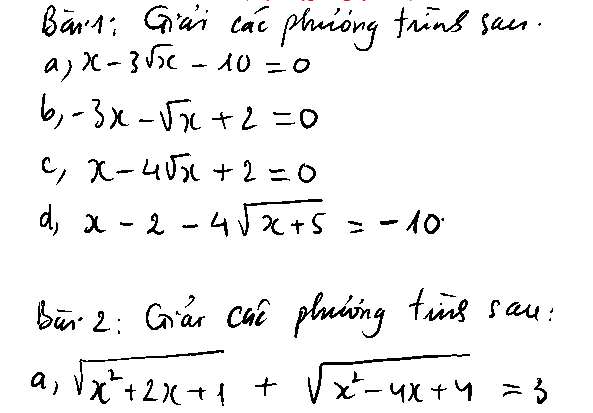
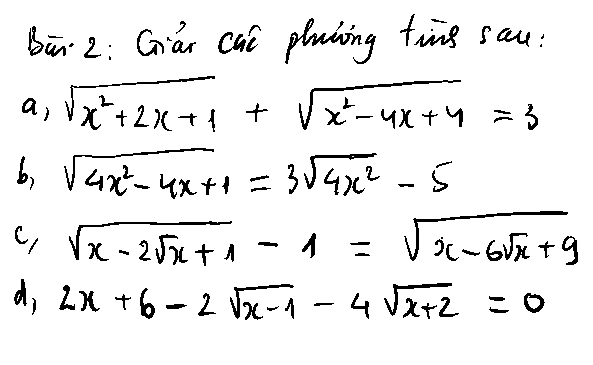
1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
a)\(\left(\left(\sqrt{x}\right)^2-2\sqrt{x}\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{49}{4}=0\)
⇒\(\left(\sqrt{x}-\dfrac{3}{2}\right)^2=\dfrac{49}{4}\)
TH1:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{7}{2}\)⇒\(\sqrt{x}=5\)⇒x=25
TH2:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{-7}{2}\)⇒\(\sqrt{x}=-2\) vì \(\sqrt{x}\)≥0 loại
giúp mik bài 1 câu c
và bài 2 câu b,c với
Câu 1:
Quy ước gen: A hạt vàng. a hạt xanh
c) ta sẽ cho cây đậu Hà Lan hạt vàng đó đi lai phân tích
- Nếu đời con đồng tính thì cá thể trội đem lai là thuần chủng.
- Nếu đời con có sự phân tính thì cá thể trội đem lai không thuần chủng
Bài 2:
Quy ước gen: A tóc xoăn. a tóc thẳng
B mắt nâu. b mắt xanh
b) kiểu gen người con trai tíc thẳng mắt xanh: aabb
-> mỗi bên P cho ra 1 loại giao tử : ab
Mà kiểu hình P:+ bố tóc xoăn mắt nâu -> kiểu gen : AaBb
+mẹ tóc thẳng mắt nâu -> kiểu gen: aaBb
c) giao tử gen bố: AB,Ab,aB,ab
Giao tử gen mẹ : aB,ab
Giúp mmk câu b. Bài 2 
- các góc đỉnh A là : \(\widehat{DAB}\) \(=\) \(52^o\) ; \(\widehat{EAB}\) \(=\) \(80^o\)
GIÚP EM BÀI 1,PHẦN B,C BÀI 2 VỚI Ạ,EM CẦN GẤP LẮM RỒIII