Tính giá trị biểu thức
a) 27,5 + 62,8 - 30,69
mình cần giải chi tiết ạ xin cảm ơn
Tính giá trị của biểu thức
a) 25,6 + 27,5×2,6 =
b) (25,6 + 27,5) ×2,6=
Tính giá trị của biểu thức
a) 25,6 + 27,5×2,6 = 25,6 + 71,5 = 97,1
b) (25,6 + 27,5) ×2,6= 53,1 x 2,6 = 138,06
Bài 1: Tính giá trị biểu thức
a) 1574,8 : 25,4 + 72 × 0,5
b) 375,42+ 95,8 × 0,1 - 207,6 nhanh chi tiết ạ !
a,=62+36
=98
b,=375,42+9,58-207,6
=385-207,6
=177,4
a)=(1574,8:25,4)+72x0,5
=62+36
=98
b)=(375,42-207,6)+(95,8x0,1)
=167,82+9,58
=177,4
a. 1574,8 : 25,4 + 72 × 0,5 b. 375,42 + 95,8 × 0,1 - 207,6
= 62 + 36 = 375,42 + 9,58 - 207,6
= 98 = 385 - 207,6
= 177,4
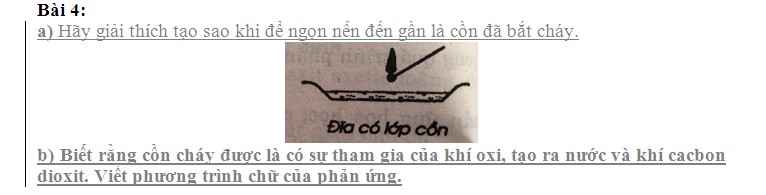 mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
Tính giá trị của biểu thức
a) 25,6 + 27,5 x 2,6 =
b) (25,6 + 27,5) x 2,6
a) 25,6 + 27,5 x 2,6 = 25,6 + 71,5 = 97,1
b) (25,6 + 27,5) x 2,6 = 53,1 x 2,6 = 138,06
có phải bạn học lớp 5E trường Đinh Tiên Hoàng đúng ko ? :)
chỉ hỏi thôi :3
a) 58, 43x12
b)50,56 : 3
mình cần giải chi tiết ạ xin cảm ơn
Bạn nào giải chi tiết hộ mình vs,mình cần tương đối gấp
Xin cảm ơn ạ
80cm=0,8m, 60cm=0,6m
Diện tích xung quanh căn phòng là:
\(2\left(10+5\right).4=120\left(m^2\right)\)
Diện tích cửa chính:
\(1,8\times2=3,6\left(m^2\right)\)
Diện tích 2 cửa sổ:
\(0,8\times0,6\times2=0,96\left(m^2\right)\)
Diện tích cần sơn:
\(200-\left(3,6+0,96\right)=115,44\left(m^2\right)\)
Chi phí tiền công:
\(195,44\times25000=2886000\) đồng
Cho \(a^2+b^2+c^2=a^3+b^3+c^3=1\)
Tính giá trị biểu thức: \(C=a^2+b^9+c^{1945}\)
Mình đang cần lời giải (chi tiết) và đang gấp. Xin giúp mình. Cảm ơn nhiều
Không mất tính tổng quát ta giả sử \(a\ge b\ge c\)
Vì \(a^2+b^2+c^2=1\Rightarrow lal,lbl,lcl\le1\)
\(\Rightarrow\hept{\begin{cases}a^2\ge a^3\\b^2\ge b^3\\c^2\ge c^3\end{cases}}\Rightarrow a^2+b^2+c^2\ge a^3+b^3+c^3=1\)
Dấu = xảy ra khi \(\hept{\begin{cases}a^2=a^3\\b^2=b^3\\c^2=c^3\end{cases}}\)
Mà theo giả thuyết thì \(\hept{\begin{cases}a\ge b\ge c\\a^2+b^2+c^2=1\end{cases}\Rightarrow\hept{\begin{cases}a=1\\b=c=0\end{cases}}}\)
Vậy C = 1
Tương tự với các trường hợp giả sử về a,b,c khác ta luôn có giá trị C = 1
Giả sử\(a\ge b\ge c\)(ko mất tính tổng quát) .Ta có :\(\hept{\begin{cases}a^2+b^2+c^2=1\\a^2;b^2;c^2\ge0\end{cases}\Rightarrow a^2;b^2;c^2\le1\Rightarrow|a|;|b|;|c|\le1\Rightarrow\hept{\begin{cases}a^2\ge a^3\\b^2\ge b^3\\c^2\ge c^3\end{cases}\Rightarrow}a^2+b^2+c^2\ge a^3+b^3+c^3=1}\)
\(\Rightarrow\hept{\begin{cases}a^2=a^3\\b^2=b^3\\c^2=c^3\end{cases}\Rightarrow\hept{\begin{cases}a,b,c\in\left\{0;1\right\}\\a^2+b^2+c^2=1\\a\ge b\ge c\end{cases}}\Rightarrow a=1;b=c=0\Rightarrow a^2+b^9+c^{1945}=1}\)
Ta có:
\(a^2+b^2+c^2=1\Rightarrow a^2,b^2,c^2\le1\)
\(\Rightarrow a,b,c\le1\)
Ta lại có: \(a^2+b^2+c^2=a^3+b^3+c^3\)
\(\Leftrightarrow a^3-a^2+b^3-b^2+c^3-c^2=0\)
\(\Leftrightarrow a^2\left(a-1\right)+b^2\left(b-1\right)+c^2\left(c-1\right)=0\)
Mà \(a^2\left(a-1\right)+b^2\left(b-1\right)+c^2\left(c-1\right)\le0\)với mọi a,b,c (vì \(a^2,b^2,c^2\le0\)và\(a,b,c\le1\))
Suy ra ta phải có: \(a^2\left(a-1\right)=b^2\left(b-1\right)=c^2\left(c-1\right)=0\)
Kết hợp gt suy ra 3 số a,b,c phải là một số bằng 1 và 2 số còn lại bằng 0.
Vì a,b,c vai trò như nhau nên giả sử \(a=1\Rightarrow b=c=0\)
Khi đó \(C=a^2+b^9+c^{1945}=1+0+0=1\)
tính giá trị của biểu thức:
a/ (7,8+4,5)x 3,6:=
b/2,25+10-4,86:1,8=
giải chi tiết giúp mk với nhé
cảm ơn trước ạ
a, (7,8+4,5) x 3,6
= 12,3 x 3,6
= 44,28
b, 2,25 + 10 - 4,86 : 1,8
= 2,25 + 10 - 2,7
= 12,25 - 2,7
= 9,55
Chúc bạn học tốt
cảm ơn bn bùi quang anh nhìu ạ
\(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\) tính giá trị biểu thức
(giải chi tiết dùm mình,cảm ơn)
\(=\sqrt{7-2\sqrt{21}+3}+\sqrt{7+2\sqrt{21}+3}\)
\(=\sqrt{\sqrt{7}^2-2\sqrt{7}.\sqrt{3}+\sqrt{3}^2}+\sqrt{\sqrt{7}^2+2\sqrt{7}.\sqrt{3}+\sqrt{3}^2}\)
\(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{7}-\sqrt{3}\right|+\left|\sqrt{7}+\sqrt{3}\right|\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=2\sqrt{7}\)
\(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=2\sqrt{7}\)
\(\sqrt{10-2\sqrt{7}}+\sqrt{10+2\sqrt{21}}\)
\(=\sqrt{3-2\sqrt{7}+7}+\sqrt{3+2\sqrt{21}+7}\)
\(=\sqrt{\sqrt{3}^2-2\sqrt{3}.\sqrt{7}+\sqrt{7}^2}+\sqrt{\sqrt{3}^2+2\sqrt{3}.\sqrt{7}+\sqrt{7}^2}\)
\(=\sqrt{\left(\sqrt{3}-\sqrt{7}\right)^2}+\sqrt{\left(\sqrt{3}+\sqrt{7}\right)^2}\)
\(=\left|\sqrt{3}-\sqrt{7}\right|+\left|\sqrt{3}+\sqrt{7}\right|\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{3}+\sqrt{7}=2\sqrt{7}\)