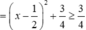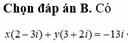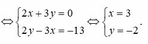Cho x,y thoả mãn : 4x2 + 17xy + 9y2 = 5xy -4Iy-2I. tính H = x3 + y3 + xy
Những câu hỏi liên quan
10) x(x-y)+x2-y2
11) x2 -y2 +10x-10y
12) x2-y2 +20x+20y
13) 4x2 -9y2-4x-6y
14) x3-y3+7x2-7y2
15) x3+4x-(y3+4y)
16) x3+y3+2x+2y
17) x3-y3-2x2y+2xy2
18) x3-4x2+4x-xy2
10: \(x\left(x-y\right)+x^2-y^2\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x+x+y\right)\)
\(=\left(x-y\right)\left(2x+y\right)\)
11: \(x^2-y^2+10x-10y\)
\(=\left(x^2-y^2\right)+\left(10x-10y\right)\)
\(=\left(x-y\right)\left(x+y\right)+10\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+10\right)\)
12: \(x^2-y^2+20x+20y\)
\(=\left(x^2-y^2\right)+\left(20x+20y\right)\)
\(=\left(x-y\right)\left(x+y\right)+20\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+20\right)\)
13: \(4x^2-9y^2-4x-6y\)
\(=\left(4x^2-9y^2\right)-\left(4x+6y\right)\)
\(=\left(2x-3y\right)\left(2x+3y\right)-2\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-2\right)\)
14: \(x^3-y^3+7x^2-7y^2\)
\(=\left(x^3-y^3\right)+\left(7x^2-7y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\cdot\left(x^2-y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+7x+7y\right)\)
15: \(x^3+4x-\left(y^3+4y\right)\)
\(=x^3-y^3+4x-4y\)
\(=\left(x^3-y^3\right)+\left(4x-4y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+4\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+4\right)\)
16: \(x^3+y^3+2x+2y\)
\(=\left(x^3+y^3\right)+\left(2x+2y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+2\right)\)
17: \(x^3-y^3-2x^2y+2xy^2\)
\(=\left(x^3-y^3\right)-\left(2x^2y-2xy^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2xy\right)\)
\(=\left(x-y\right)\left(x^2-xy+y^2\right)\)
18: \(x^3-4x^2+4x-xy^2\)
\(=x\left(x^2-4x+4-y^2\right)\)
\(=x\left[\left(x^2-4x+4\right)-y^2\right]\)
\(=x\left[\left(x-2\right)^2-y^2\right]\)
\(=x\left(x-2-y\right)\left(x-2+y\right)\)
Đúng 0
Bình luận (0)
Tính giá trị biểu thức sau:
a) A=x3+15x2+75x+125 Với x= -10
b) B=4x2+12xy+9y2 Tại x=1;y=2
c) C=27x3-27x2y+9xy2-y3 Với x=1;y= -2
Giải chi tiết giúp mình nha.Cảm ơn
\(a,A=\left(x+5\right)^3=\left(-10+5\right)^3=\left(-5\right)^3=-125\\ b,B=\left(2x+3y\right)^2=\left(2\cdot1+3\cdot2\right)^2=7^2=49\\ c,C=\left(3x-y\right)^3=\left(3\cdot1+2\right)^3=5^3=125\)
Đúng 3
Bình luận (0)
Cho 2 số x,y thoả mãn: \(4x^2+17xy+9y^2=5xy-\left|y-2\right|\)
Tính giá trị biểu thức \(M=x^3+2y+3x^2y\)
Ta thấy \(4x^2+17xy+9y^2=5xy-\left|y-2\right|\)
\(\Leftrightarrow4x^2+12xy+9y^2=-\left|y-2\right|\Leftrightarrow\left(2x+3y\right)^2=-\left|y-2\right|\)
Do \(\left(2x+3y\right)^2\ge0;-\left|y-2\right|\le0\) nên dấu bằng xảy ra khi và chỉ khi \(\hept{\begin{cases}y-2=0\\2x+3y=0\end{cases}}\Rightarrow\hept{\begin{cases}y=2\\x=-3\end{cases}}\)
Thay vào M ta có \(M=\left(-3\right)^3+2.2+3.\left(-3\right)^2.2=31\)
Đúng 0
Bình luận (0)
Cho hai số thực x,y thay đổi thoả mãn x+y1. Giá trị nhỏ nhất của
x
3
+
y
3
+
2
x
y
bằng A.
-
1
4
B.
1
4
C.
5
4
D.
3
4
Đọc tiếp
Cho hai số thực x,y thay đổi thoả mãn x+y=1. Giá trị nhỏ nhất của x 3 + y 3 + 2 x y bằng
A. - 1 4
B. 1 4
C. 5 4
D. 3 4
Cho các số thực x,y thoả mãn x+y=2.Tìm giá trị nhỏ nhất của biểu thức:
A= x3 + y3 + 3x2y2
A=(x+y)3 - 3xy(x+y)+3x2y2
=8-6xy+3x2y2
=3(x2y2-2xy+1)+5
=3(xy+1)2+5 ≥5
dấu = xảy ra ⇔ xy=1 ⇒ x=y=1
Đúng 1
Bình luận (0)
Tìm các số thực x, y thoả mãn
x
2
-
3
i
+
y
3
+
2
i
-
13
i
với i là đơn vị ảo.
Đọc tiếp
Tìm các số thực x, y thoả mãn x 2 - 3 i + y 3 + 2 i = - 13 i với i là đơn vị ảo.
Bài 1. Làm tính nhân:a) 3x2 (2 - 5xy) b) -dfrac{2}{3} xy (xy2 - x3 + 4) c) ( x - 7 y )( xy + 1)Bài 2. Rút gọn các biểu thức sau:a) 5x(4x2 - 2x +1) - 2x(10x2 - 5x - 2)b) 3x( x - 2) - 5x(1- x) - 8(x2 - 3)d) (x3 - 2x)(x2 +1)
Đọc tiếp
Bài 1. Làm tính nhân:
a) 3x2 (2 - 5xy)
b) -\(\dfrac{2}{3}\) xy (xy2 - x3 + 4)
c) ( x - 7 y )( xy + 1)
Bài 2. Rút gọn các biểu thức sau:
a) 5x(4x2 - 2x +1) - 2x(10x2 - 5x - 2)
b) 3x( x - 2) - 5x(1- x) - 8(x2 - 3)
d) (x3 - 2x)(x2 +1)
Bài 1:
\(a,6x^2-15x^3y\\ b,=-\dfrac{2}{3}x^2y^3+\dfrac{2}{3}x^4y-\dfrac{8}{3}xy\)
Bài 2:
\(a,=20x^3-10x^2+5x-20x^3+10x^2+4x=9x\\ b,=3x^2-6x-5x+5x^2-8x^2+24=24-11x\\ c,=x^5+x^3-2x^3-2x=x^5-x^3-2x\)
Đúng 1
Bình luận (0)
câu d của bài 2 là của bài 1 nha mình để nhầm chỗ huhu
Đúng 0
Bình luận (0)
Cho 4x^2+17xy+9y^2=5xy-4|y-z|
Tính A=x^3+y^3+xy
Nhanh nha mik đang cần gấp
Cho các số thực x,y thoả mãn x+y 2.Tìm giá trị nhỏ nhất của biểu thức: A x3�3 + y3�3 + x2�2 + y2
Đọc tiếp
Cho các số thực x,y thoả mãn x+y =2.Tìm giá trị nhỏ nhất của biểu thức: A= + + +
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
Đúng 0
Bình luận (0)