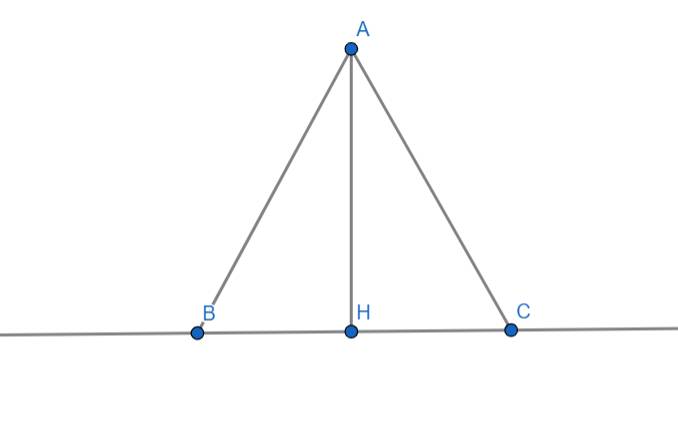
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a.Gọi H là hình chiếu của điểm A xuống đường thẳng a.Trên đường thẳng a lấy 2 điểm B và C .Tính độ dài đường xiên AB,AC.Biết AH=6cm,HB=8cm,HC=10cm.

Những câu hỏi liên quan
cho đường thằng a và điểm A nằm ngoài đường thẳng a. gọi H là hình chiếu của điểm A xuống đường thẳng a. trên đường thẳng a lấy hai điểm B và C. tính độ dài các đường xiên AB; AC biết AH= 6cm; HB= 8cm; HC= 10cm
Cho đường thẳng a và điểm A nằm ngoài đường thẳng. Gọi H là hình chiếu của điểm A xuống đường thẳng a. Trên đường thẳng a lấy 2 điểm B và C tính rộ dài đường xiên AB, AC biết AM=6cm, HB=8cm, HC=10cm
cho đường thẳng a và điểm A nằm ngoài đường thẳng a gọi H là hình chiếu của điểm A xuống đường thẳng a trên a lấy 2 diểm B&C tính AB;AC biết AH=6cm ;HB=8cm; HC=10cm
Vì AH là đường chiếu
=)) AH vuông góc vs a
Xét tam giác AHB ( góc H = 90 độ ) có :
AB2 = AH2 + HB2 ( Theo Đ/lý Pi-ta-go )
=) AB2 = 62 + 82
=) AB2 = 36 + 64
=) AB2 = 100
=) AB = \(\sqrt{100}\)
=) AB = 10
Xét tam giác AHC ( góc H = 90 độ ) có :
AC2 = AH2 + HC2 ( Theo Đ/lý Pi-ta-go )
=) AC2 = 62 + 102
=) AC2 = 36 + 100
=) AC2 = 136
=) AC = \(\sqrt{136}\)
=) AC = 11,7
Vậy AB = 10 ; AC = 11,7
Đúng 0
Bình luận (0)
Bài 1: Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Gọi H là hình chiếu của A
trên đường thẳng a. Trên đường thẳng a lấy hai điểm B và C. Gọi D là trung điểm của AH.
Biết HB = 8cm; HC = 10cm; AH = 6cm.
a. So sánh AB và AC; b. So sánh BD và AC.
a) Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=6^2+8^2=100\)
hay AB=10(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=6^2+10^2=136\)
hay \(AC=2\sqrt{34}cm\)
Ta có: AB=10cm
\(AC=2\sqrt{34}cm\)
mà \(10cm< 2\sqrt{34}cm\)
nên AB<AC
Đúng 0
Bình luận (0)
Cho đường thẳng a và điểm A nằm ngoài đường thẳng a.Gọi H là hình chiếu của A trên đường thẳng a.Trên a lấy 2 điểm B và C.Tính độ dài các đường xiên AB và AC biết AH=6cm,HB=8cm,HC=10cm
Bài 1 : Cho đường thẳng a và điểm A nằm ngoài đường thẳng a . Trên đường thẳng a lấy hai điểm B và C . Tính độ dài các đường xiên AB , AC biết AH6cm ; HB8cm ; HC10cmBài 2 :Cho tam giác ABC ( AB khác AC) Gọi M là một điểm nằm giữa B và C. Gọi E lần lượt là hình chiếu của B và C xuống đường thẳng AM. So sánh BE+CF với BCBài 3 : Cho tam giác ABC có 3 góc nhọn . Kẻ BD vuông góc với AC ( D thuộc AC ), CE vuông góc với AB ( E thuộc AB ). Chứng minh BD+CEAB+ACGIÚP MÌNH VỚI !!! TỐI THỨ BẢY NHÉ MỌI NGƯỜI...
Đọc tiếp
Bài 1 : Cho đường thẳng a và điểm A nằm ngoài đường thẳng a . Trên đường thẳng a lấy hai điểm B và C . Tính độ dài các đường xiên AB , AC biết AH=6cm ; HB=8cm ; HC=10cm
Bài 2 :Cho tam giác ABC ( AB khác AC) Gọi M là một điểm nằm giữa B và C. Gọi E lần lượt là hình chiếu của B và C xuống đường thẳng AM. So sánh BE+CF với BC
Bài 3 : Cho tam giác ABC có 3 góc nhọn . Kẻ BD vuông góc với AC ( D thuộc AC ), CE vuông góc với AB ( E thuộc AB ). Chứng minh BD+CE<AB+AC
GIÚP MÌNH VỚI !!! TỐI THỨ BẢY NHÉ MỌI NGƯỜI NHỚ VẼ HÌNH NHÉ CÁC BẠN
cho đoạn thẳng a vad điểm A nằm ngoài a. Gọi H là hình chiếu của điểm A xuống đường thẳng a. Trên đường thẳng a lấy B sao cho Ah = 6cm, HB = 8cm , HC= 10cm
Tính AB, AC
Hai đường xiên AB và AC kẻ từ điểm A xuống đường thẳng BC có hình chiếu lần lượt là HB và HC. Nếu AB nhỏ hơn AC thì: A: HC>HB B: HC
Xét ΔABC có AB<AC(gt)
mà hình chiếu của AB trên BC là HB
và hình chiếu của AC trên BC là HC
nên HC>HB
Đúng 0
Bình luận (0)
từ một điểm A nằm ngoài đường thẳng d , vẽ đường vuông góc AH và các đường xiên AB,AC tùy ý
b) c/m : Nếu AB =AC thì HB=HC ; ngược lại , nếu HB=HC thì AB=AC
`@ AB = AC`
Xét `\triangle ABH` vuông tại `H` và `\triangle ACH` vuông tại `H` có:
`{:(AB=AC),(AH\text{ là cạnh chung}):}}=>\triangle ABH =\triangle ACH` (ch+1cgv)
`=>HB=HC` (`2` cạnh t/ứ)
`@HB=HC`
Chứng mình tương tự giống trường hợp trên.
Đúng 5
Bình luận (2)