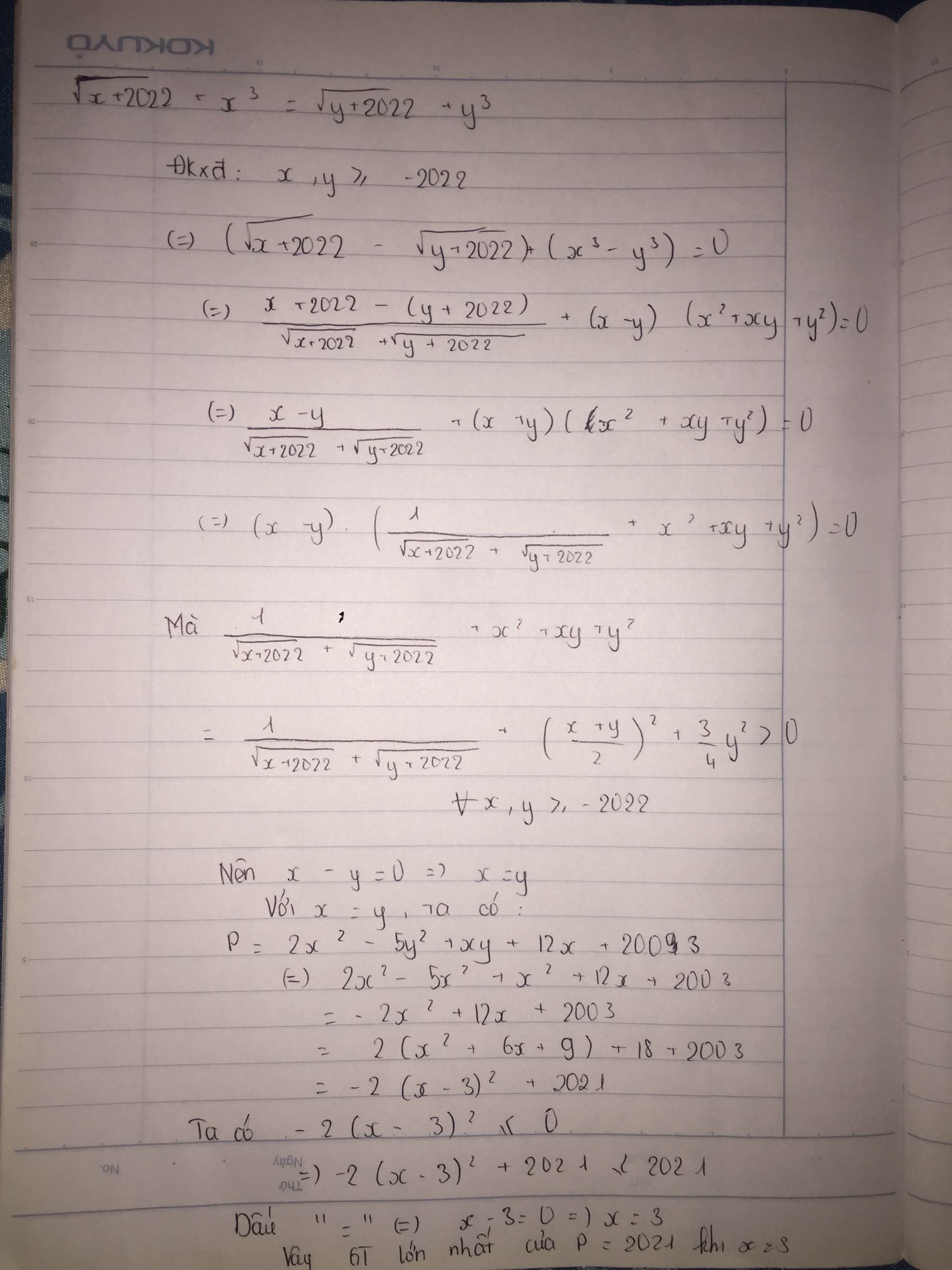12x + 16 = 2020 ![]()

Những câu hỏi liên quan
Tìm x biết:
1,
a,3x(x+1) - 2x(x+2) = -x-1
b,2x(x-2020) - x+2020 = 0
c,(x-4)2 - 36 = 0
d,x2 + 8x - 16 = 0
e,x(x+6) - 7x - 42 = 0
f,25x2 - 16 = 0
2,
a,3x3 - 12x = 0
b,x2 + 3x - 10 = 0
Bài 1:
a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)
\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)
b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)
e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cần gấp !!!
Cho \(\sqrt{x+2020}+x^3=\sqrt{y+2020}+y^3\) Tìm giá trị lớn nhất \(P=2x^2-5y^2+xy+12x+2003\)
tinh B =X^17-12X^16+12X^15+...-12X^2+12X-1
cho x^2-x=1.tinh b=x^6-3x^5+5x^4+5x^3-6x^2-12x+2020
Cho x,y là các số thực thỏa mãn : (x+\(\sqrt{x^2+\sqrt{2020}}\))( y+ \(\sqrt{y^2+\sqrt{2020}}\)) =\(\sqrt{2020}\)
Tìm Min M=9x4+7y4-12x2+4y2+5
Theo đề bài:
\(\left(x+\sqrt{x^2+\sqrt{2020}}\right)\left(y+\sqrt{y^2+\sqrt{2020}}\right)=\sqrt{2020}\)(1)
Lại có: \(\left(x+\sqrt{x^2+\sqrt{2020}}\right)\left(\sqrt{x^2+\sqrt{2020}}-x\right)=\sqrt{2020}\)(2)
Và \(\left(\sqrt{y^2+\sqrt{2020}}-y\right)\left(y+\sqrt{y^2+\sqrt{2020}}\right)=\sqrt{2020}\)(3)
Từ (1) và (3) => \(x+\sqrt{x^2+\sqrt{2020}}=\sqrt{y^2+\sqrt{2020}}-y\)
<=> \(x+y=-\sqrt{x^2+\sqrt{2020}}+\sqrt{y^2+\sqrt{2020}}\)(4)
Từ (1) và (2) => \(\sqrt{x^2+\sqrt{2020}}-x=\sqrt{y^2+\sqrt{2020}}+y\)
<=> \(x+y=\sqrt{x^2+\sqrt{2020}}-\sqrt{y^2+\sqrt{2020}}\)(5)
Từ (4) ( 5 ) => x + y = - ( x + y ) <=> x = - y
=> \(M=9x^4+7x^4-12x^2+4x^2+5\)
\(=16x^4-8x^2+5=\left(4x^2-1\right)^2+4\ge4\)
Dấu "=" xảy ra <=> \(4x^2-1=0\)<=> \(x=\pm\frac{1}{2}\)
Với x = 1/2 => (x; y) = ( 1/2; -1/2)
Với x = -1/2 => ( x; y ) = ( -1/2; 1/2)
Vậy min M = 4 đạt tại ....
Tính B = x^17 - 12x^16 + 12x^15 - 12x^14 +... - 12x^2 + 12x -1
với x=11
làm nhanh giùm mk với
Bạn thay 12 = x + 1 vào B rồi khai triển ra nó sẽ tự triệt tiêu hết
Đúng 0
Bình luận (0)
Tính giá trị của đa thức:
A=x19-12x18+12x17-12x16+...+12x-1 tại x=11
Cho \(S=\frac{1}{16}+\frac{2}{16^2}+\frac{3}{16^3}+...+\frac{2020}{16^{2020}}\). So sánh: \(S^{2020}\) và \(S^{2021}\).
1 bài trong đề thi HSG lớp 9 nhằm giúp các bạn học sinh lớp 9 ôn lại kiến thức lớp 6
\(S^{2020}\)và\(S^{2021}\)?Thế này sai mất thui.
Vì \(2020< 2021\)nên\(S^{2020}< S^{2021}\).
The Angry sai rồi
Nên chú ý rằng với một số \(S>0\)và \(m,n\in N,m>n\)thì:
Nếu \(0< S< 1\)thì \(S^m< S^n\)
Nếu \(S\ge1\)thì \(S^m\ge S^n\)
Bạn chưa chỉ ra khoảng giá trị của \(S\)thì không thể kết luận được.
Xem thêm câu trả lời
a=2020. 2020-2022.2018
b= (1/4 -1).(1/9-1).(1/16-1)....(1/400-1)
a) $2020.2020-2022.2018$
$ = 2020^2-(2020+2).(2020-2)$
$ = 2020^2 - (2020^2-2^2)$
$ = 4$
b) \(\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\left(\dfrac{1}{16}-1\right)...\left(\dfrac{1}{400}-1\right)\)
\(=\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)\left(\dfrac{1}{4^2}-1\right)...\left(\dfrac{1}{20^2}-1\right)\)
\(=\dfrac{\left(-1\right)\cdot3\cdot\left(-2\right)\cdot4\cdot\left(-3\right)\cdot5\cdot\cdot\cdot\left(-19\right)\cdot21}{2^2\cdot3^2\cdot4^2\cdot\cdot\cdot20^2}\)
\(=-\dfrac{1}{20}\cdot\dfrac{21}{2}=-\dfrac{21}{40}\)
Đúng 2
Bình luận (0)
Giải:
a) 2020.2020−2022.2018
=20202−(2020+2).(2020−2)
=20202−(20202−22)
=4
b) =(1/22−1)(1/32−1)(1/42−1)...(1/202-1)
=−1/20⋅21/2
Đúng 1
Bình luận (0)