Làm giúp mình câu 3 hình với ạ, mình cảm ơn :3

Những câu hỏi liên quan

Ai giúp mình phần 2 nhỏ bài tìm gtri nguyên n với câu 3 bài hình đc ko ạ(kèm vẽ hình) nếu cần thiết mn làm giúp e câu 5 ạ ko thì thôi ạ. Mình cảm ơn nhiều
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Đúng 2
Bình luận (0)
Mọi người ơi giúp mình làm câu 2 và câu 3 với ạ!! Mình xin cảm ơn rất nhiều ạ!
Ai giúp mình làm 3 câu này với ạ mình đang cần gấp. Cảm ơn mn nhiều ạ.
Giúp mình làm Câu c) bài hình và bài cuối với ạ, mình cảm ơn :3
Nhanh một chút ạ, mình đang cần

Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)
Đúng 1
Bình luận (3)
Câu 5:
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\sqrt{1+x}+\sqrt{1-x}=t>0\)
\(\Rightarrow t^2=1+x+1-x+2\sqrt{\left(1+x\right)\left(1-x\right)}=2+2\sqrt{1-x^2}\)
Do đó pt trở thành:
\(t.t^2=8\Leftrightarrow t^3=8\)
\(\Leftrightarrow t=2\Leftrightarrow\sqrt{1-x}+\sqrt{1+x}=2\)
\(\Leftrightarrow2+2\sqrt{1-x^2}=4\Leftrightarrow\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=1\)
\(\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
Đúng 2
Bình luận (3)
Ai giúp mình làm câu 3 với, mình đang cần gấp để nộp ạ. Cảm ơn mn nhiều.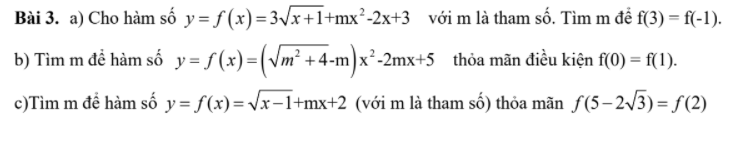
c: \(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+m\left(5-2\sqrt{3}\right)+2=\sqrt{2-1}+2m+2\)
\(\Leftrightarrow\sqrt{3}+1+m\left(5-2\sqrt{3}\right)=2m+3\)
\(\Leftrightarrow m\left(3-2\sqrt{3}\right)=2-\sqrt{3}\)
hay \(m=-\dfrac{\sqrt{3}}{3}\)
Đúng 0
Bình luận (0)

Giúp em với ạ vẽ hình nữa làm mình câu a) cũng được ạ em cảm ơn nhìu ::)>>33
a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)
Đúng 2
Bình luận (0)
ai giúp mình với minh cảm ơn nhìu ạ. làm câu nào nào cũng được ạ mình cảm ơn 
Giúp mình 3 câu với ạ mình cảm ơn 














