Tính đạo hàm của hàm số y=6x

Những câu hỏi liên quan
Tính đạo hàm của hàm số sau:
y
(
2
x
3
-
3
x
2
+
6
x
+
1
)
2
A.
2
2
x
3
-
x
2
+
6
x
+
1...
Đọc tiếp
Tính đạo hàm của hàm số sau: y = ( 2 x 3 - 3 x 2 + 6 x + 1 ) 2
A. 2 2 x 3 - x 2 + 6 x + 1 6 x 2 - 6 x + 6
B. 2 2 x 3 - 3 x 2 + x + 1 x 2 - 6 x + 6
C. 2 2 x 3 - 3 x 2 + 6 x + 1 x 2 - 6 x + 6
D. 2 2 x 3 - 3 x 2 + 6 x + 1 6 x 2 - 6 x + 6
- Sử dụng công thức ( u α ) ' với
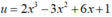 .
.
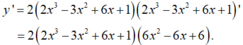
Chọn D.
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau: y (2x3 – 3x2 – 6x + 1)2. A. 2(2x3 – x2 + 6x + 1)(6x2 – 6x + 6) B. 2(2x3 - 3x2 + x + 1)(x2 – 6x + 6) C. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6) D. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
Đọc tiếp
Tính đạo hàm của hàm số sau: y = (2x3 – 3x2 – 6x + 1)2.
A. 2(2x3 – x2 + 6x + 1)(6x2 – 6x + 6)
B. 2(2x3 - 3x2 + x + 1)(x2 – 6x + 6)
C. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
D. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp ![]() với u = 2x3 – 6x + 1
với u = 2x3 – 6x + 1
y' = 2(2x3 – 3x2 + 6x + 1)(2x3 – 3x2 + 6x + 1)’ = 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6).
Đúng 0
Bình luận (0)
Đạo hàm của hàm số
y
2
x
2
-
6
x
bằng: A.
1
2
2
x
2
-
6
x
B.
2
x
-
6...
Đọc tiếp
Đạo hàm của hàm số y = 2 x 2 - 6 x bằng:
A. 1 2 2 x 2 - 6 x
B. 2 x - 6 2 x 2 - 6 x
C. - 2 x - 3 2 2 x 2 - 6 x
D. 2 x - 3 2 2 x 2 - 6 x
Tính các đạo hàm của hàm số sau:
a) \(y=\sqrt{x}\left(x+3\right)\)
b) \(y=\sqrt{2x^2-6x-9}\)
c) \(y=\left(\sqrt{x^2+1}+x\right)^{10}\)
tính đạo hàm của các hàm số sau
a) \(y=x^2+3x-6x^6+\dfrac{2x-3}{x-1}\)
b) \(y=3x^2-4x+\sqrt{2x^2-3x+1}\)
c) \(y=\sqrt{4x^2-3x+1}-4\)
a: \(y'=\left(x^2\right)'+\left(3x\right)'-\left(6x^6\right)'+\left(\dfrac{2x-3}{x-1}\right)'\)
\(=2x+3-6\cdot6x^5+\dfrac{\left(2x-3\right)'\left(x-1\right)-\left(2x-3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{2\left(x-1\right)-2x+3}{\left(x-1\right)^2}\)
\(=-36x^5+2x+3+\dfrac{1}{\left(x-1\right)^2}\)
b: \(\left(\sqrt{2x^2-3x+1}\right)'=\dfrac{\left(2x^2-3x+1\right)'}{2\sqrt{2x^2-3x+1}}\)
\(=\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(y'=3\cdot2x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
\(=6x-4+\dfrac{4x-3}{2\sqrt{2x^2-3x+1}}\)
c: \(\left(\sqrt{4x^2-3x+1}\right)'=\dfrac{\left(4x^2-3x+1\right)'}{2\sqrt{4x^2-3x+1}}\)
\(=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
\(y'=\left(\sqrt{4x^2-3x+1}\right)'-4'=\dfrac{8x-3}{2\sqrt{4x^2-3x+1}}\)
Đúng 1
Bình luận (0)
Cho hàm số \(u = \sin x\) và hàm số \(y = {u^2}\).
a) Tính \(y\) theo \(x\).
b) Tính \(y{'_x}\) (đạo hàm của \(y\) theo biến \(x\)), \(y{'_u}\) (đạo hàm của \(y\) theo biến \(u\)) và \(u{'_x}\) (đạo hàm của \(u\) theo biến \(x\)) rồi so sánh \(y{'_x}\) với \(y{'_u}.u{'_x}\).
a: \(y=u^2=\left(sinx\right)^2\)
b: \(y'\left(x\right)=\left(sin^2x\right)'=2\cdot sinx\cdot cosx\)
\(y'\left(u\right)=\left(u^2\right)'=2\cdot u\)
\(u'\left(x\right)=\left(sinx\right)'=cosx\)
=>\(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)
Đúng 1
Bình luận (0)
Cho hàm số \(y = {x^{22}}\)
a) Tính đạo hàm của hàm số trên tại điểm x bất kì
b) Tính đạo hàm của hàm số trên tại điểm \({x_0} = - 1\)
a) Ta có: \(f'\left( x \right) = \left( {{x^{22}}} \right)' = 22.{x^{21}}\)
b) Đạo hàm của hàm số tại điểm \({x_0} = - 1\) là: \(f'\left( { - 1} \right) = 22.{\left( { - 1} \right)^{21}} = - 22\)
Đúng 0
Bình luận (0)
Dùng định nghĩa tính đạo hàm của hàm số y = x 3 tại điểm x tùy ý.
Dự đoán đạo hàm của hàm số y = x 100 tại điểm x.
- Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:
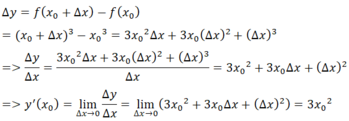
- Dự đoán đạo hàm của y = x100 tại điểm x là 100x99
Đúng 0
Bình luận (0)
Cho hàm số
y
π
x
.
x
π
. TÍnh đạo hàm y’ của hàm số. A.
y
x
π
.
π
x
-
1
π
+
xln
π
B.
y
π...
Đọc tiếp
Cho hàm số y = π x . x π . TÍnh đạo hàm y’ của hàm số.
A. y ' = x π . π x - 1 π + xln π
B. y ' = π x . x π - 1 xln π - π
C. y ' = π x . x π - 1 xln π + π
D. y ' = π x . x π - 1 π - xln π
Ta có
y ' = π x ' . x π + π x . x π ' = π x . x π - 1 π + xln π
Đáp án C
Đúng 0
Bình luận (0)










