- Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:
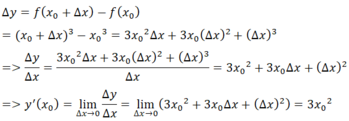
- Dự đoán đạo hàm của y = x100 tại điểm x là 100x99
- Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:
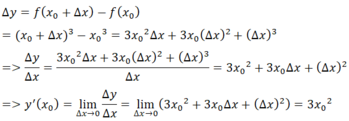
- Dự đoán đạo hàm của y = x100 tại điểm x là 100x99
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm x 0 ?
A. lim x → 0 f x + ∆ x - f x 0 ∆ x
B. lim x → 0 f x - f x 0 x - x 0
C. lim x → x 0 f x - f x 0 x - x 0
D. lim x → 0 f x + ∆ x - f x ∆ x
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm x 0 ?
A. lim x → 0 f x + ∆ x - f x 0 ∆ x
B. lim x → 0 f x - f x 0 x - x 0
C. lim x → x 0 f x - f x 0 x - x 0
D. lim x → 0 f x + ∆ x - f x ∆ x
Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: y = x 2 + x tại x 0 = 1
Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: y = x + 1 x - 1 tại x 0 = 0
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Bằng định nghĩa, hãy tính đạo hàm của các hàm số:
a) f x = x 2 tại điểm x bất kì;
b) g x = 1 / x tại điểm bất kì x ≠ 0
Tính đạo hàm của hàm số y = 2 x 2 + x + 1 tại điểm x= 2
A. 9
B. 4
C. 7
D. 6
Phát biểu định nghĩa đạo hàm của hàm số y = f x tại x = x o .