Chọn C.
- Theo định nghĩa đạo hàm tại điểm x = x 0 .
Chọn C.
- Theo định nghĩa đạo hàm tại điểm x = x 0 .
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm x 0 ?
A. lim x → 0 f x + ∆ x - f x 0 ∆ x
B. lim x → 0 f x - f x 0 x - x 0
C. lim x → x 0 f x - f x 0 x - x 0
D. lim x → 0 f x + ∆ x - f x ∆ x
Cho hàm số f x = x 2 n ế u x ≥ 0 x 2 - 1 n ế u x < 0
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
b) Dùng định nghĩa chứng minh định nghĩa trên
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
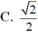
D. 1
Cho hàm số f ( x ) = 3 - 4 - x 4 k h i x ≢ 0 1 4 k h i x = 0 . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Cho hàm số y = f x = a x 5 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 . Biết f'(-1)=3 . Tính lim ∆ x → 0 f 1 + ∆ x - f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Tìm a,b để hàm số f ( x ) = x 2 + 1 k h i x ≥ 0 2 x 2 + a x + b k h i x < 0 có đạo hàm tại x = 0?
A. a = 10; b = 11
B. a = 0; b = -1
C. a = 0; b = 1
D. a = 20; b = 1
Tìm a,b để hàm số f ( x ) = x 2 + 1 k h i x ≥ 0 2 x 2 + a x + b k h i x < 0 có đạo hàm tại x = 0?
A. a = 10, b = 11
B. a = 0, b = -1
C. a = 0, b = 1
D. a = 20, b = 1
#HELP
Hình bên là đồ thị của một hàm số y=f(x) y=f(x) , f(x) f(x) không xác định tại x = -1 x=−1 . Dự đoán \lim\limits_{x\rightarrow-1}f\left(x\right) x→−1 lim f(x) .
#THANKS _YOU