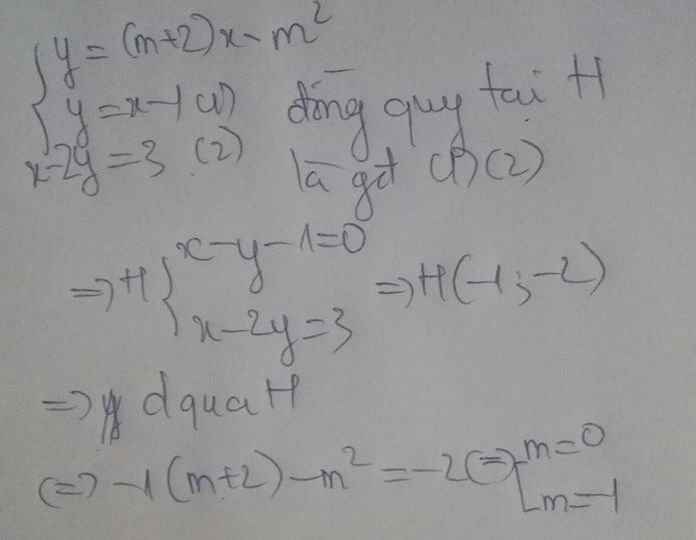tìm m để hai đường thẳng y = ( m2 - 1 )x + 2 và y = 2(m + 1)x+1 có hệ số góc bằng nhau

Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng (d):y=x 6 và (dm ):y=(m2-3m 3)x m2 m(với m là tham số)
1)Tìm m để đường thẳng (dm) đi qua điểm M(-1;1)
2)Tìm m để đường thẳng (dm) song song với đường thẳng (d).Với giá trị m và tìm được, hãy tí...
Xem chi tiết
1.a) Vẽ đồ thị hàm số y‐2x+3y‐2x+3 và tính góc của đường thẳng tạo với trục Ox b) Tìm m để đường thẳng yx+m2+1yx+m2+1 và đường thẳng y(m+1)x+5ym+1x+5 cắt nhau tại một điểm trên trục tung 2.Trong đợt quyên góp ủng hộ miền Trung bị bão lụt của trường THCS Đà Nẵng , lớp 9a và 9b quyên góp được 1105000 đồng .Mỗi học sinh lớp 9a đống góp 10000đồng , mỗi học sinh lớp 9b quyên góp 15000đồng .Gọi số học sinh lớp 9a là x và số học sinh lớp 9b là y a. em viết hệ thức biểu diễn y theo xb. nếu số học sinh...
Đọc tiếp
1.a) Vẽ đồ thị hàm số y=‐2x+3y=‐2x+3 và tính góc của đường thẳng tạo với trục Ox b) Tìm m để đường thẳng y=x+m2+1y=x+m2+1 và đường thẳng y=(m+1)x+5y=m+1x+5 cắt nhau tại một điểm trên trục tung 2.Trong đợt quyên góp ủng hộ miền Trung bị bão lụt của trường THCS Đà Nẵng , lớp 9a và 9b quyên góp được 1105000 đồng .Mỗi học sinh lớp 9a đống góp 10000đồng , mỗi học sinh lớp 9b quyên góp 15000đồng .Gọi số học sinh lớp 9a là x và số học sinh lớp 9b là y a. em viết hệ thức biểu diễn y theo xb. nếu số học sinh lớp 9a là 43 . tính số học sinh lớp 9b
Cho đường thẳng (d): y=(m+2)x-m2 (m là tham số) .Tìm m để đường thẳng (d) và các đường thẳng y=x-1 ; x-2y=3 cắt nhau tại 1 điểm.
Ta có: y=x-1
nên x-1=y
=>x-y=1
Tọa độ giao điểm của hai đường x-y=1 và x-2y=3 là:
\(\left\{{}\begin{matrix}x-y=1\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Thay x=-1 và y=-2 vào y=(m+2)x-m2, ta được:
\(-m^2+\left(-1\right)\cdot\left(m+2\right)=-2\)
\(\Leftrightarrow-m^2-m-2=-2\)
\(\Leftrightarrow m^2+m=0\)
=>m=0 hoặc m=-1
Đúng 5
Bình luận (0)
`x-2y=3<=>y=1/2x-3/2`
Xét hệ ptr:`{(y=x-1),(y=1/2x-3/2):}`
`<=>{(1/2x+1/2=0<=>x=-1),(y=-1-1=-2):}`
Để `(d)` cắt các đường thẳng `y=x-1` và `x-2y=3` tại `1` điểm thì `3` đường thẳng này phải đồng quy
Tức là: `x=-1;y=-2` thuộc `(d)`
`=>-2=(m+2).(-1)-m^2`
`<=>m^2+m=0`
`<=>m(m+1)=0`
`<=>m=0` hoặc `m=-1`
Vậy `m={0;-1}`
Đúng 1
Bình luận (0)
1) Cho 2 hàm số y-x+1 và y3x + 2 .a) vẽ đồ thị 2 hàm số trên cùng 1 hệ trục tọa độ .b) Tính góc tạo bởi 2 đường thẳng đó trên trục hoành2) Cho đường thẳng (d) có phương trình y m+1.x-3m+6.Tìm m,n để: .â) (d) // với đường thẳng -2x+5 và đi qua điểm có tọa độ (2 ; -1).b) (d) tạo bởi trục hoành 1 góc tù .c) (d) có hệ số góc bằng -2 và trung độ góc bằng 1.3) Cho hàm số y(m+3).+2m+1 (d1) và y2m.x-3m-4 (d2) â) Tìm m để d1 cắt d2, d1 song song với d2, d1 trùng d2.b) d1 và d2 cắt nhau tại 1 điểm trên...
Đọc tiếp
1) Cho 2 hàm số y=-x+1 và y=3x + 2 .
a) vẽ đồ thị 2 hàm số trên cùng 1 hệ trục tọa độ .
b) Tính góc tạo bởi 2 đường thẳng đó trên trục hoành
2) Cho đường thẳng (d) có phương trình y = m+1.x-3m+6.Tìm m,n để: .
â) (d) // với đường thẳng -2x+5 và đi qua điểm có tọa độ (2 ; -1).
b) (d) tạo bởi trục hoành 1 góc tù .
c) (d) có hệ số góc bằng -2 và trung độ góc bằng 1.
3) Cho hàm số y=(m+3).+2m+1 (d1) và y=2m.x-3m-4 (d2)
â) Tìm m để d1 cắt d2, d1 song song với d2, d1 trùng d2.
b) d1 và d2 cắt nhau tại 1 điểm trên trục trung .
c) d1 và d2 cắt nhau tại 1 điểm trên trục hoành .
đ) Tìm góc tạo bởi 2 đường thẳng với trục Ox khi m =-1
Bài 2. Cho hàm số y(m−1)x+n có đồ thị là đường thẳng d
a) Tìm m và n để đường thẳng d đi qua hai điểm A(1;2), B(2;5).
b) Tìm m và n biết đường thẳng d có hệ số góc bằng 3, cắt trục hoành tại điểm có hoành độ bằng –2.
c) Tìm m và n biết đường thẳng d trùng với đường thẳng d:y5x-3.
Bài 3. a) Cho hai đường thẳng d:y(m-3)x-3m+3, d, :y(2m+1)x+m+5
Tìm m để hai đường thẳng cắt nhau; song song với nhau; vuông góc với nhau; trùng nhau; cắt nhau tại một điểm nằm trên trục tung.
b) Tìm m để ba đường...
Đọc tiếp
Bài 2. Cho hàm số y=(m−1)x+n có đồ thị là đường thẳng d a) Tìm m và n để đường thẳng d đi qua hai điểm A(1;2), B(2;5). b) Tìm m và n biết đường thẳng d có hệ số góc bằng 3, cắt trục hoành tại điểm có hoành độ bằng –2. c) Tìm m và n biết đường thẳng d trùng với đường thẳng d:y=5x-3. Bài 3. a) Cho hai đường thẳng d:y=(m-3)x-3m+3, d, :y=(2m+1)x+m+5 Tìm m để hai đường thẳng cắt nhau; song song với nhau; vuông góc với nhau; trùng nhau; cắt nhau tại một điểm nằm trên trục tung. b) Tìm m để ba đường thẳng d:y=2x+5,d:y=x+2,d :y=mx−12 đồng quy
2
a)
d đi qua A (1;2), B(2;5)
=> Ta có hệ phương trình: \(\left\{{}\begin{matrix}\left(m-1\right).1+n=2\\\left(m-1\right).2+n=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+n=3\\2m+n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=-1\end{matrix}\right.\)
b)
d có hệ số góc a = 3 => d: y = 3x + n
=> m -1 = 3 <=> m = 4
d cắt Ox tại x = -2, y = 0 \(\Leftrightarrow0=3.\left(-2\right)+n\) => n = 6
c)
d trùng d' \(\Rightarrow\left\{{}\begin{matrix}m-1=5\\n=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=6\\n=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1) Giải hệ phương trình sau:
$left{begin{array}{l}dfrac{2}{x-y}+sqrt{y+1}4 dfrac{1}{x-y}-3 sqrt{y+1}-5end{array}right.$.
2) Cho Parabol $(P): yx^{2}$ và đường thẳng $(d): y2(m-1) x-m^{2}+2 m$ ($m$ là tham số)
a) Tìm tọa độ giao điểm của Parabol $(P)$ và đường thẳng $(d)$ khi $m2$.
b) Tìm $m$ để đường thẳng $(d)$ và Parabol $(P)$ cắt nhau tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ đối nhau.
Đọc tiếp
1) Giải hệ phương trình sau:
$\left\{\begin{array}{l}\dfrac{2}{x-y}+\sqrt{y+1}=4 \\ \dfrac{1}{x-y}-3 \sqrt{y+1}=-5\end{array}\right.$.
2) Cho Parabol $(P): y=x^{2}$ và đường thẳng $(d): y=2(m-1) x-m^{2}+2 m$ ($m$ là tham số)
a) Tìm tọa độ giao điểm của Parabol $(P)$ và đường thẳng $(d)$ khi $m=2$.
b) Tìm $m$ để đường thẳng $(d)$ và Parabol $(P)$ cắt nhau tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ đối nhau.
1) ĐK \(\hept{\begin{cases}x\ne y\\y\ge-1\end{cases}}\)
Đặt \(\hept{\begin{cases}\frac{1}{x-y}=a\left(a\ne0\right)\\\sqrt{y+1}=b\left(b\ge0\right)\end{cases}}\)hệ phương trình đã cho trở thành
\(\hept{\begin{cases}2a+b=4\\a-3b=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+b=4\\2a-6b=-10\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=14\\2a+b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\end{cases}\left(tm\right)}\)
\(\Rightarrow\hept{\begin{cases}\frac{1}{x-y}=1\\\sqrt{y+1}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=1\\y+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}\left(tm\right)\)
Vậy ...
ĐKXĐ:
x
≠
y
;
y
≥
−
1
Đặt
1
x
−
y
=
a
;
√
y
+
1
=
b
(ĐK:
a
≠
0
;
b
≥
0
)
Khi đó hệ phương trình trở thành
{
2
a
+
b
=
4
a
−
3
b
=
−
5
⇔
{
6
a
+
3
b
=
12
a
−
3
b
=
−
5
⇔
{
7
a
=
7
b
=
4
−
2
a
⇔
{
a
=
1
(
tm
)
b
=
2
(
tm
)
Với
⎧
⎪
⎨
⎪
⎩
a
=
1
b
=
2
⇒
⎧
⎪
⎨
⎪
⎩
1
x
−
y
=
1
√
y
+
1
=
2
⇒
{
x
−
y
=
1
y
+
1
=
4
⇔
{
x
−
3
=
1
y
=
3
⇔
{
x
=
4
(
tm
)
y
=
3
(
tm
)
Vậy hệ phương trình đã cho có nghiệm
{
x
=
4
y
=
3
.
2) Xét phương trình hoành độ giao điểm giữa đường thẳng
(
d
)
và Parabol
(
P
)
là:
x
2
=
2
(
m
−
1
)
x
−
m
2
+
2
m
⇔
x
2
−
2
(
m
−
1
)
x
+
m
2
−
2
m
=
0
(1)
a) Với
m
=
2
phương trình (1) trở thành:
x
2
−
2
(
2
−
1
)
x
+
2
2
−
2.2
=
0
⇔
x
2
−
2
x
=
0
⇔
x
(
x
−
2
)
=
0
⇔
[
x
=
0
x
=
2
- Với
x
=
0
⇒
y
=
0
2
=
0
⇒
A
(
0
;
0
)
- Với
x
=
2
⇒
y
=
2
2
=
4
⇒
B
(
2
;
4
)
Vậy khi
m
=
2
thì
(
P
)
cắt
(
d
)
tại hai điểm phân biệt
A
(
0
;
0
)
;
B
(
2
;
4
)
.
b) Ta có:
Δ
′
=
b
′
2
−
a
c
=
[
−
(
m
−
1
)
]
2
−
(
m
2
−
2
m
)
=
m
2
−
2
m
+
1
−
m
2
+
2
m
=
1
>
0
Do
Δ
′
>
0
nên phương trình (1) luôn có hai nghiệm phân biệt
x
1
;
x
2
với mọi
m
.
⇒
Đường thẳng
(
d
)
luôn cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ
x
1
;
x
2
với mọi
m
.
Khi đó theo hệ thức Viet, ta có:
{
x
1
+
x
2
=
2
m
−
2
x
1
x
2
=
m
2
−
2
m
Để đường thẳng
(
d
)
cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ đối nhau
⇔
x
1
+
x
2
=
0
⇔
2
m
−
2
=
0
⇔
m
=
1
(
tm
)
Vậy
m
=
1
thì đường thẳng
(
d
)
luôn cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ đối nhau.
ĐKXĐ:
x
≠
y
;
y
≥
−
1
Đặt
1
x
−
y
=
a
;
√
y
+
1
=
b
(ĐK:
a
≠
0
;
b
≥
0
)
Khi đó hệ phương trình trở thành
{
2
a
+
b
=
4
a
−
3
b
=
−
5
⇔
{
6
a
+
3
b
=
12
a
−
3
b
=
−
5
⇔
{
7
a
=
7
b
=
4
−
2
a
⇔
{
a
=
1
(
tm
)
b
=
2
(
tm
)
Với
⎧
⎪
⎨
⎪
⎩
a
=
1
b
=
2
⇒
⎧
⎪
⎨
⎪
⎩
1
x
−
y
=
1
√
y
+
1
=
2
⇒
{
x
−
y
=
1
y
+
1
=
4
⇔
{
x
−
3
=
1
y
=
3
⇔
{
x
=
4
(
tm
)
y
=
3
(
tm
)
Vậy hệ phương trình đã cho có nghiệm
{
x
=
4
y
=
3
.
2) Xét phương trình hoành độ giao điểm giữa đường thẳng
(
d
)
và Parabol
(
P
)
là:
x
2
=
2
(
m
−
1
)
x
−
m
2
+
2
m
⇔
x
2
−
2
(
m
−
1
)
x
+
m
2
−
2
m
=
0
(1)
a) Với
m
=
2
phương trình (1) trở thành:
x
2
−
2
(
2
−
1
)
x
+
2
2
−
2.2
=
0
⇔
x
2
−
2
x
=
0
⇔
x
(
x
−
2
)
=
0
⇔
[
x
=
0
x
=
2
- Với
x
=
0
⇒
y
=
0
2
=
0
⇒
A
(
0
;
0
)
- Với
x
=
2
⇒
y
=
2
2
=
4
⇒
B
(
2
;
4
)
Vậy khi
m
=
2
thì
(
P
)
cắt
(
d
)
tại hai điểm phân biệt
A
(
0
;
0
)
;
B
(
2
;
4
)
.
b) Ta có:
Δ
′
=
b
′
2
−
a
c
=
[
−
(
m
−
1
)
]
2
−
(
m
2
−
2
m
)
=
m
2
−
2
m
+
1
−
m
2
+
2
m
=
1
>
0
Do
Δ
′
>
0
nên phương trình (1) luôn có hai nghiệm phân biệt
x
1
;
x
2
với mọi
m
.
⇒
Đường thẳng
(
d
)
luôn cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ
x
1
;
x
2
với mọi
m
.
Khi đó theo hệ thức Viet, ta có:
{
x
1
+
x
2
=
2
m
−
2
x
1
x
2
=
m
2
−
2
m
Để đường thẳng
(
d
)
cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ đối nhau
⇔
x
1
+
x
2
=
0
⇔
2
m
−
2
=
0
⇔
m
=
1
(
tm
)
Vậy
m
=
1
thì đường thẳng
(
d
)
luôn cắt Parabol
(
P
)
tại hai điểm phân biệt có hoành độ đối nhau.
Xem thêm câu trả lời
1) Giải hệ phương trình $left{begin{array}{l}2 sqrt{x}+dfrac{3}{y-1}5 4 sqrt{x}-dfrac{1}{y-1}3end{array}right.$
2) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): yx^{2}$ và đường thẳng $(d): ym x-1$, với $m$ là tham số ($m neq 0$)
a) Khi $m3$, tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$.
b) Tìm tất cả các giá trị khác 0 của tham số $m$ để đường thẳng $(d)$ cắt parabol $(P)$ tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ thỏa mãn $x_{2}(x_{1}^{2}+1)3$.
Đọc tiếp
1) Giải hệ phương trình $\left\{\begin{array}{l}2 \sqrt{x}+\dfrac{3}{y-1}=5 \\ 4 \sqrt{x}-\dfrac{1}{y-1}=3\end{array}\right.$
2) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): y=x^{2}$ và đường thẳng $(d): y=m x-1$, với $m$ là tham số ($m \neq 0$)
a) Khi $m=3$, tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$.
b) Tìm tất cả các giá trị khác 0 của tham số $m$ để đường thẳng $(d)$ cắt parabol $(P)$ tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ thỏa mãn $x_{2}(x_{1}^{2}+1)=3$.
1) ĐK \(\hept{\begin{cases}x\ge0\\y\ne1\end{cases}}\)
Đặt \(\hept{\begin{cases}2\sqrt{x}=a\left(a\ge0\right)\\\frac{1}{y-1}=b\left(b\ne0\right)\end{cases}}\)hệ phương trình đã cho trở thành
\(\hept{\begin{cases}a+3b=5\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+6b=10\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=7\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}\left(tm\right)}\)
\(\Rightarrow\hept{\begin{cases}2\sqrt{x}=2\\\frac{1}{y-1}=1\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\left(tm\right)\)
Vậy ...
1,\(\left\{{}\begin{matrix}2\sqrt{x}+\dfrac{3}{y-1}=5\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\) ĐKXĐ:x≥o,y≠1
⇔\(\left\{{}\begin{matrix}4\sqrt{x}+\dfrac{6}{y-1}=10\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-1}=7\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\4\sqrt{x}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\left(TM\right)\)
vậy hpt đã cho có nghiệm duy nhất (x,y)=(1,2)
2,a, xét pthđgđ của (d) và (p) khi m=3:
x\(^2\)=3x-1⇔\(x^2-3x+1=0\)
Δ=(-3)\(^2\)-4.1.1=5>0
⇒pt có 2 nghiệm pb
\(x_1=\dfrac{3+\sqrt{5}}{2}\) ,\(x_2=\dfrac{3-\sqrt{5}}{2}\)
thay x=x\(_1\)=\(\dfrac{3+\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:
y=(\(\dfrac{3+\sqrt{5}}{2}\))\(^2\)=\(\dfrac{14+6\sqrt{5}}{4}\)⇒A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\))
thay x=x\(_2\)=\(\dfrac{3-\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:
y=\(\left(\dfrac{3-\sqrt{5}}{2}\right)^2=\dfrac{14-6\sqrt{5}}{4}\)⇒B(\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))
vậy tọa độ gđ của (d) và (p) là A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\)) và B (\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))
b,xét pthđgđ của (d) và (p) :
\(x^2=mx-1\)⇔\(x^2-mx+1=0\) (*)
Δ=(-m)\(^2\)-4.1.1=m\(^2\)-4
⇒pt có hai nghiệm pb⇔Δ>0
⇔m\(^2\)-4>0⇔m>16
với m>16 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)
theo hệ thức Vi-ét ta có:
(I) \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=1\end{matrix}\right.\)
\(x_1,x_2\) TM \(x_2\)(x\(_1\)\(^2\)+1)=3
⇒\(x_2.x_1^2\)+\(x_2\)=3⇔\(x_2.x_1.x_1+x_2=3\)⇔(\(x_2.x_1\))(\(x_1+x_2\))=3 (**)
thay (I) vào (**) ta được:
1.m=3⇔m=3 (TM m≠0)
vậy m=3 thì (d) cắt (p) tại hai điểm pb có hoanh độ \(x_1.x_2\) TM \(x_2\)(\(x_1^2+1\))=3
1) a) Tính giá trị của biểu thức \(\sqrt{\left(\sqrt{3}-2\right)^2}\)+\(\sqrt{3}\)
b) Tìm các giá trị của tham số m để hai đường thẳng (d):y=(m+2).x-m (m≠-2) và (d'):y = -2x-2m+1 cắt nhau.
c) Tìm hệ số góc của đường thẳng (d):y=(2m-3)x+m ( với m≠\(\dfrac{3}{2}\)) biết (d) đi qua điểm A (3;-1)
a) √(√3 - 2)² + √3
= 2 - √3 + √3
= 2
b) Để (d) và (d') cắt nhau thì:
m + 2 ≠ -2
m ≠ -2 - 2
m ≠ -4
Vậy m ≠ -4 thì (d) cắt (d')
c) Thay tọa độ điểm A(3; -1) vào (d) ta có:
(2m - 3).3 + m = -1
⇔ 6m - 9 + m = -1
⇔ 7m = -1 + 9
⇔ 7m = 8
⇔ m = 8/7 (nhận)
Thay m = 8/7 vào (d) ta có:
(d): y = -5x/7 - 8/7
Vậy hệ số góc của (d) là -5/7
Đúng 2
Bình luận (0)
EM CẦN GẤP Ạ..GIÚP EM VỚI Ạ..
1)Cho hàm số y=(m-1)x+m (d)
a)Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1
b)Chứng minh (d) luôn đi qua 1 điểm cố định với mọi m
2)Cho 3 đường thẳng d1:y=x-2;d2:y=2-x;d3:y=(2-m)x+1.Tính góc tạo bởi đường thẳng d1 và trục Ox