 Câu b nha
Câu b nha

Những câu hỏi liên quan
mn giúp mik với nha. Câu b thui nha mn.
Đọc tiếp

mn giúp mik với nha. Câu b thui nha mn.
b: Xét ΔABH vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
Xét ΔAHB vuông tại H có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{5}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{12}{5}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{5}{12}\)
Đúng 0
Bình luận (0)
giải bài 2 câu b hộ mình chỉ câu b thôi nha vẽ hình luôn

Giải giúp em câu b với, câu b thôi nha. Em cảm ơn nhiều ạ! 
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
Đúng 2
Bình luận (1)
Câu k cuối câu là (a^2 +b^2 ) nha
\(\left(a^2+ab+b^2\right)\left(a^2-ab+b^2\right)-\left(a^4+b^4\right)\)
\(=\left[\left(a^2+b^2\right)^2-a^2b^2\right]-\left(a^4+b^4\right)\)
\(=a^4+b^4+2a^2b^2-a^2b^2-a^4-b^4\)
\(=a^2b^2\)
Đúng 0
Bình luận (0)
giúp mình câu b với d nha , câu b là tính góc k1, mình cảm ơn 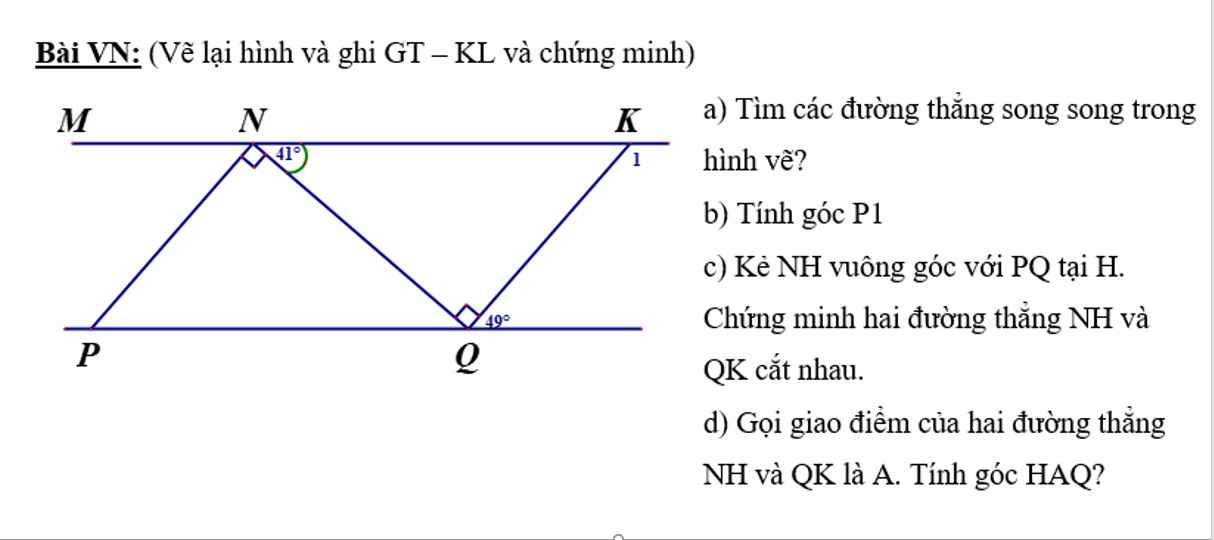
câu b nha mn
giúp câu b Nha
Đọc tiếp
giúp câu b Nha
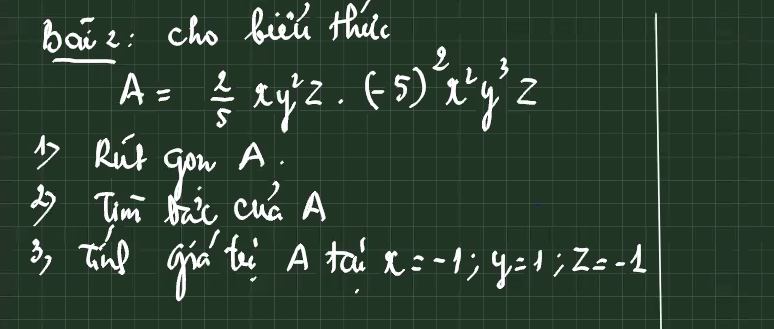 CÂU B THOI NHA
CÂU B THOI NHA
\(1)\)
\(A = \dfrac{2}{5}xy^2z . ( -5 )x^2y^3z\)
\(A = [\dfrac{2}{5} . ( -5 )] . ( x . x^2 ) . ( y^2 . y^3 ) . ( z . z )\)
\(A = -2x^3y^5z^2\)
\(2)\)
\(-\) Bậc của \(A : 3 + 5 + 2 = 10\)
Vậy \(, \) bậc của đơn thức \(A \) là \(10\)
\(3)\)
Thay \(x = -1 ; y = 1 ; z = -1 \) vào bt \(A\) ta có \(:\)
\(A = -2 . ( -1 )^3 . 1^5 . ( -1 )^2\)
\(A = -2 ; ( -1 ) . 1 . 1\)
\(A = 2\)
Vậy \(, A = 2 \) tại \(x = -1 ; y = 1 ; z = -1 \)
Đúng 2
Bình luận (0)
giải cho mình câu b ,c và d thôi nha
giải cách làm nha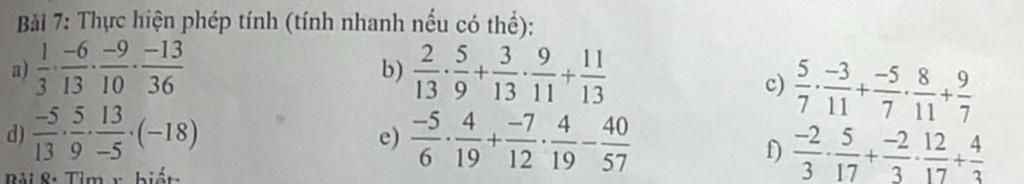
b: \(=\dfrac{1}{13}\left(\dfrac{10}{9}+\dfrac{27}{11}\right)+\dfrac{11}{13}=\dfrac{1}{13}\cdot\dfrac{353}{99}+\dfrac{11}{13}=\dfrac{1442}{1287}\)
c: \(=\dfrac{-5}{7}\left(\dfrac{3}{11}+\dfrac{8}{11}\right)+\dfrac{9}{7}=\dfrac{-5}{7}+\dfrac{9}{7}=\dfrac{4}{7}\)
d: \(=\dfrac{-5}{-5}\cdot\dfrac{13}{13}\cdot\dfrac{5}{9}\cdot\left(-18\right)=\dfrac{5}{9}\cdot\left(-18\right)=-10\)
Đúng 1
Bình luận (0)

















