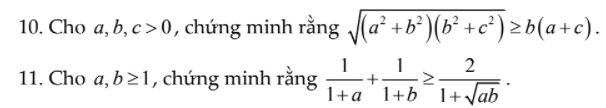Câu nèo thé ?_?

Câu nào thế bạn????

where is câu hỏi???

Theo gt ta có: $n_{KCl}=0,2(mol)$

a, $2KClO_3\rightarrow 2KCl+3O_2$ (đk: nhiệt độ, MnO_2$

b, Ta có: $n_{O_2}=0,3(mol)\Rightarrow V_{O_2}=6,72(l)$

c, Ta có: $n_{S}=0,1(mol)$

$S+O_2\rightarrow SO_2$

Sau phản ứng $O_2$ sẽ dư 0,2mol

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:

\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)

Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)

2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)

\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)

câu 3 chứ

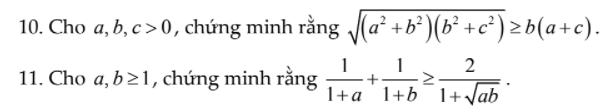10. Câu này chứng minh BĐT BSC:

\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)

11.

Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)

\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)

\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)

\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)

\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)

Đẳng thức xảy ra khi \(a=b=1\)

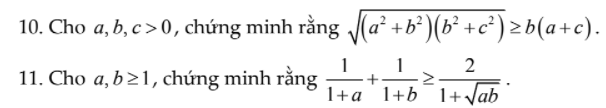
dùng phương pháp hình học cm câu a 

đặt BH =a , HC =c kẻ HA =b 

theo định lí py ta go ta có 

AB=a²+b²;AC=b²+c²;BC=a+b

dễ thấy AB.AC\(\ge\) 2SABC=BC.AH

(a²+b²).(b²+c²)\(\ge\)b.(a+c)

\(\dfrac{12}{16}=\dfrac{132}{176}\\ \dfrac{13}{16}=\dfrac{143}{176}\\ Ta.có:\dfrac{16}{22}< \dfrac{132}{176}< \dfrac{17}{22}< \dfrac{143}{176}< \dfrac{18}{22}\\ Vậy:Chọn.số.17\)