giải pt
6x4+25x3+12x2-25x+6 = 0
Giai cac pt:
a) x4 -3x3 + 4x2 -3x+1 =0
b) 6x4 + 5x3 -38x2 +5x +6 = 0
c) 3x4 -13x3 +16x2 -13x+3 =0
d)6x4 + 7x3 -36x2 - 7x +6 =0
e) 6x4 +25x3 + 12x2 -25x +6 =0
Tính giá trị của thức:
M=x10-25x9+25x8-25x7+...-25x3+25x2-25x+25 với x = 24
Lời giải:
$M=(x^{10}-24x^9)-(x^9-24x^8)+(x^8-24x^7)-(x^7-24x^6)+(x^6-24x^5)-(x^5-24x^4)+(x^4-24x^3)-(x^3-24x^2)+(x^2-24x)-(x-24)+1$
$=x^9(x-24)-x^8(x-24)+x^7(x-24)-.....+x(x-24)-(x-24)+1$
$=(x-24)(x^9-x^8+x^7-...+x-1)+1$
$=0.(x^9-x^8+....+x-1)+1=1$
Tính giá trị của biểu thức:
M=x10-25x9+25x8-25x7+...-25x3+25x2-25x+25 với x=24
\(M=x^{10}-25x^9+25x^8-25x^7+...-25x^3+25x^2-25x+25\)
Ta thấy : \(x=24\Rightarrow x+1=25\)
\(\Rightarrow M=x^{10}-\left(x+1\right)x^9+\left(x+1\right)x^8-\left(x+1\right)x^7+...-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+\left(x+1\right)\)
\(M=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...-x^4-x^3+x^3+x^2-x^2-x+x+1\)
\(\Rightarrow M=1\)
Vậy \(M=1\left(tạix=24\right)\)
M=x
10
−25x
9
+25x
8
−25x
7
+...−25x
3
+25x
2
−25x+25
Ta thấy :
x
=
24
⇒
x
+
1
=
25
x=24⇒x+1=25
⇒
M
=
x
10
−
(
x
+
1
)
x
9
+
(
x
+
1
)
x
8
−
(
x
+
1
)
x
7
+
.
.
.
−
(
x
+
1
)
x
3
+
(
x
+
1
)
x
2
−
(
x
+
1
)
x
+
(
x
+
1
)
⇒M=x
10
−(x+1)x
9
+(x+1)x
8
−(x+1)x
7
+...−(x+1)x
3
+(x+1)x
2
−(x+1)x+(x+1)
M
=
x
10
−
x
10
−
x
9
+
x
9
+
x
8
−
x
8
−
x
7
+
.
.
.
−
x
4
−
x
3
+
x
3
+
x
2
−
x
2
−
x
+
x
+
1
M=x
10
−x
10
−x
9
+x
9
+x
8
−x
8
−x
7
+...−x
4
−x
3
+x
3
+x
2
−x
2
−x+x+1
⇒
M
=
1
⇒M=1
Vậy
M
=
1
(
t
ạ
i
x
=
24
)
M=1(tạix=24)
Cho hàm số f x = 1 3 x 3 - 1 2 x 2 - 4 x + 6
Giải phương trình f"(cos x) = 0
Cho hàm số
f x = 1 3 x 3 - 1 2 x 2 - 4 x + 6
Giải phương trình f'(sin x) = 0.
Giải phương trình: \(6x^4+25x^3+12x^2-25x+6=0\)
Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(6\left(x^2+\frac{1}{x^2}\right)+25\left(x-\frac{1}{x}\right)+12=0\)
Đặt \(x-\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2+2\)
\(\Rightarrow6\left(t^2+2\right)+25t+12=0\)
\(\Leftrightarrow6t^2+25t+24=0\Rightarrow\left[{}\begin{matrix}t=-\frac{3}{2}\\t=-\frac{8}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-\frac{1}{x}=-\frac{3}{2}\\x-\frac{1}{x}=-\frac{8}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x^2+3x-2=0\\3x^2+8x-3=0\end{matrix}\right.\)
Giải pt: 6x4 + 25x3 + 12x2 - 25x + 6 = 0
đây là pt đỗi xứng bậc chẵn bạn ơi
cos cachs giải đó bạn
(+) Kiểm tra x = 0 , sau đó chia cả hai vế cho x^2
(+) đặt x- 1/x = a => x^2 + 1/x^2 = a^2 + 2
Thay vô giải pt bậc hai
à ha , tự nhiên tui quên mất ^^! , thks nhá , k cần giải nữa đâu , bik giải gòi
Giải các phương trình: 3x4 – 12x2 + 9 = 0
Cả ba phương trình trên đều là phương trình trùng phương.
3x4 – 12x2 + 9 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 3t2 – 12t + 9 = 0 (2)
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1 và t2 = 3.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x2 = 3 ⇒ x = ±√3.
+ t = 1 ⇒ x2 = 1 ⇒ x = ±1.
Vậy phương trình có tập nghiệm 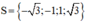
Bài 1 :Phân tích đa thức sau thành nhân tử
(12x2+6x)(y+z)+(12x2+6x)(y-z)
Bài 2:tìm x:
x(x-6)+10(x-6)=0
1.
\(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\\ =\left(12x^2+6x\right)\left(y+z+y-z\right)\\ =2y\left(12x^2+6x\right)\\ =2y.6x\left(2x+1\right)\\ =12xy\left(2x+1\right)\)
2.
\(x\left(x-6\right)+10\left(x-6\right)=0\\ \Leftrightarrow\left(x-6\right)\left(x+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
Vậy \(x\in\left\{6;-10\right\}\) là nghiệm của pt
Bài 1:
Ta có: \(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\)
\(=\left(12x^2+6x\right)\left(y+z+y-z\right)\)
\(=6x\left(2x+1\right)\cdot2y\)
\(=12xy\left(2x+1\right)\)
Bài 2:
Ta có: \(x\left(x-6\right)+10\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)