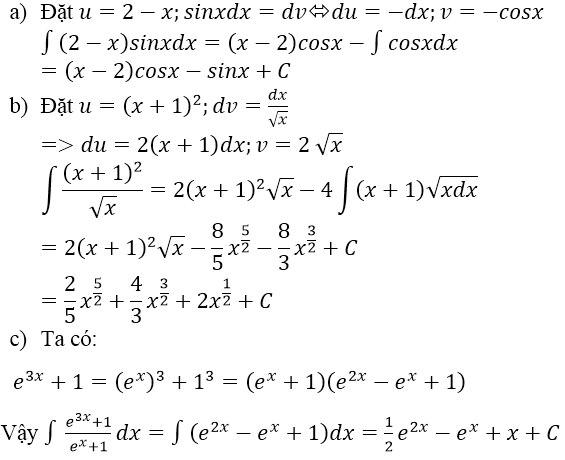\(I=\int\dfrac{x}{1-cos2x}dx=\int\dfrac{x}{2sin^2x}dx\)

Đặt \(\left\{{}\begin{matrix}u=\dfrac{x}{2}\\dv=\dfrac{1}{sin^2x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{2}\\v=-cotx\end{matrix}\right.\)

\(\Rightarrow I=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int cotxdx=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{cosx.dx}{sinx}\)

\(=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{d\left(sinx\right)}{sinx}=\dfrac{-x.cotx}{2}+\dfrac{1}{2}ln\left|sinx\right|+C\)

2/ Câu 2 bữa trước làm rồi, bạn coi lại nhé

3/ \(I=\int\left(2x+1\right)ln^2xdx\)

Đặt \(\left\{{}\begin{matrix}u=ln^2x\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{2lnx}{x}dx\\v=x^2+x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x\right)ln^2x-\int\left(2x+2\right)lnxdx=\left(x^2+x\right)ln^2x-I_1\)

\(I_1=\int\left(2x+2\right)lnx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=lnx\\dv=\left(2x+2\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=x^2+2x\end{matrix}\right.\)

\(\Rightarrow I_1=\left(x^2+2x\right)lnx-\int\left(x+2\right)dx=\left(x^2+2x\right)ln-\dfrac{x^2}{2}+2x+C\)

\(\Rightarrow I=\left(x^2+x\right)ln^2x-\left(x^2+2x\right)lnx+\dfrac{x^2}{2}-2x+C\)

4/ \(I=\int\left(2x-1\right)cosx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x-1\\dv=cosx.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=sinx\end{matrix}\right.\)

\(\Rightarrow I=\left(2x-1\right)sinx-2\int sinx.dx=\left(2x-1\right)sinx+2cosx+C\)

5/ \(I=\int\left(x^2+x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=x^2+x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\left(2x+1\right)dx\\v=e^x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x+1\right)e^x-\int\left(2x+1\right)e^xdx\)

\(I_1=\int\left(2x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=e^x\end{matrix}\right.\)

\(\Rightarrow I_1=\left(2x+1\right)e^x-2\int e^xdx=\left(2x+1\right)e^x-2e^x+C=\left(2x-1\right)e^x+C\)

\(\Rightarrow I=\left(x^2+x+1\right)e^x-\left(2x-1\right)e^x+C=\left(x^2-x+2\right)e^x+C\)

6/ \(I=\int\left(2x+1\right).ln\left(x+2\right)dx\)

\(\Rightarrow\left\{{}\begin{matrix}u=ln\left(x+2\right)\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x+2}\\v=x^2+x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x\right)ln\left(x+2\right)-\int\dfrac{x^2+x}{x+2}dx\)

\(=\left(x^2+x\right)ln\left(x+2\right)-\int\left(x-1+\dfrac{2}{x+2}\right)dx\)

\(I=\left(x^2+x\right)ln\left(x+2\right)-\dfrac{x^2}{2}+x-2ln\left|x+2\right|+C\)

a) Đặt \(\sqrt{2x-5}=t\) khi đó \(x=\frac{t^2+5}{2}\) , \(dx=tdt\)

Do vậy \(I_1=\int\frac{\frac{1}{4}\left(t^2+5\right)^2+3}{t^3}dt=\frac{1}{4}\int\frac{\left(t^4+10t^2+37\right)t}{t^3}dt\)

                \(=\frac{1}{4}\int\left(t^2+10+\frac{37}{t^2}\right)dt=\frac{1}{4}\left(\frac{t^3}{3}+10t-\frac{37}{t}\right)+C\)

Trở về biến x, thu được :

\(I_1=\frac{1}{12}\sqrt{\left(2x-5\right)^3}+\frac{5}{2}\sqrt{2x-5}-\frac{37}{4\sqrt{2x-5}}+C\)

b) \(I_2=\frac{1}{3}\int\frac{d\left(\ln\left(3x-1\right)\right)}{\ln\left(3x-1\right)}=\frac{1}{3}\ln\left|\ln\left(3x-1\right)\right|+C\)

c) \(I_3=\int\frac{1+\frac{1}{x^2}}{\sqrt{x^2-7+\frac{1}{x^2}}}dx=\int\frac{d\left(x-\frac{1}{x}\right)}{\sqrt{\left(x-\frac{1}{2}\right)^2-5}}\)

Đặt \(x-\frac{1}{x}=t\)

\(\Rightarrow\) \(I_3=\int\frac{dt}{\sqrt{t^2-5}}=\ln\left|t+\sqrt{t^2-5}\right|+C\)

                           \(=\ln\left|x-\frac{1}{x}+\sqrt{x^2-7+\frac{1}{x^2}}\right|+C\)

Chịu thôi khó quá.

a) \(f\left(x\right)=\frac{3x^2+3x+12}{\left(x-1\right)\left(x+2\right)x}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{x}=\frac{Ax\left(x+2\right)+Bx\left(x-1\right)+C\left(x-1\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)x}\)

Bằng cách thay các nghiệm thực của mẫu số vào hai tử số, ta có hệ :

\(\begin{cases}x=1\rightarrow18=3A\Leftrightarrow A=6\\x=-2\rightarrow18=6B\Leftrightarrow B=3\\x=0\rightarrow12=-2C\Leftrightarrow=-6\end{cases}\) \(\Rightarrow f\left(x\right)=\frac{6}{x-1}+\frac{3}{x+2}-\frac{6}{x}\)

Vậy : \(\int\frac{3x^2+3x+12}{\left(x-1\right)\left(x+2\right)x}dx=\int\left(\frac{6}{x-1}+\frac{3}{x+2}-\frac{6}{x}\right)dx=6\ln\left|x-1\right|+3\ln\left|x+2\right|-6\ln\left|x\right|+C\)

b) \(f\left(x\right)=\frac{x^2+2x+6}{\left(x-1\right)\left(x-2\right)\left(x-4\right)}=\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{x-4}\)

\(=\frac{A\left(x-2\right)\left(x-4\right)+B\left(x-1\right)\left(x-4\right)+C\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)\left(x-4\right)}\)

Bằng cách thay các nghiệm của mẫu số vào hai tử số ta có hệ :

\(\begin{cases}x=1\rightarrow9A=3\Leftrightarrow x=3\\x=2\rightarrow14=-2B\Leftrightarrow x=-7\\x=4\rightarrow30=6C\Leftrightarrow C=5\end{cases}\)

\(\Rightarrow f\left(x\right)=\frac{3}{x-1}-\frac{7}{x-2}+\frac{5}{x-4}\)

Vậy :

\(\int\frac{x^2+2x+6}{\left(x-1\right)\left(x-2\right)\left(x-4\right)}dx=\)\(\int\left(\frac{3}{x-1}+\frac{7}{x-2}+\frac{5}{x-4}\right)dx\)=\(3\ln\left|x-1\right|-7\ln\left|x-2\right|+5\ln\left|x-4\right|+C\)

Biến đổi: ʃ\(\int\dfrac{1dx}{cosx\dfrac{\sqrt{2}}{2}\left(cosx-sinx\right)}=\int\dfrac{\sqrt{2}dx}{cos^2x\left(1-tanx\right)}=\int\dfrac{\sqrt{2}d\left(tanx\right)}{1-tanx}=-\sqrt{2}\ln trituyetdoi\left(1-tanx\right)\)

https://www.youtube.com/channel/UCzeAuHrGhk8hUszunoNtayw

Luyện Thi THPT Quốc Gia miễn phí 100%