Giải phương trình:
(x+1)x(x2+x+1)=42
Giải các phương trình:
a x - 3 2 + x + 4 2 = 23 − 3 x b ) x 3 + 2 x 2 − x - 3 2 = ( x − 1 ) x 2 − 2 c ) x - 1 3 + 0 , 5 x 2 = x x 2 + 1 , 5 d ) x ( x − 7 ) 3 − 1 = x 2 − x − 4 3 e ) 14 x 2 − 9 = 1 − 1 3 − x f ) $ 2 x x + 1 = x 2 − x + 8 ( x + 1 ) ( x − 4 )
a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
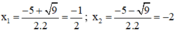
Vậy phương trình có tập nghiệm 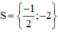
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
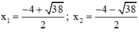
Vậy phương trình có tập nghiệm 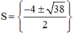
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
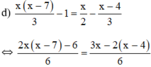
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
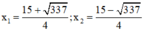
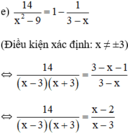
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
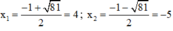
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
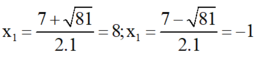
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
Giải các phương trình sau:
a) 201 − x 99 + 203 − x 97 + 205 − x 95 + 3 = 0 ;
b) x 2 + x + 4 2 + x 2 + x + 7 3 = x 2 + x + 13 5 + x 2 + x + 16 6 Gợi ý: Bớt 3.
a ) x = 300
b) Gợi ý: Bớt 3 ở từng phân số. Đáp số: x = 1; x = -2
1) Giải phương trình: x(x-3)-(x+2)(x-1)=3 ta được nghiệm
2) Phương trình nào sau đây có 1 nghiệm
a) x(x-1)=0 b) (x+2)(x2+1)=0
c) x2-3x=0 d) x2-2x+3=0
1. x(x-3)-(x+2)(x-1)=3 <=> x2 - 3x - x2 - x + 2 = 3 => 4x = -1 => x = 1/4
2.
a) x = 0, x=1 (2 nghiệm, loại)
b) x2 + 1 > 0 => x = - 2 (1 nghiệm, chọn b)
c) <=> x(x-3) = 0 => x = 0, x=3 (2 nghiệm, loại)
d) (x-1)2 + 2 > 0 => Vô nghiệm (loại)
Giải phương trình: 2x2 -1/ x3 +1 + 1/x+1 = 2x (1- x2 -x/ x2 -x +1 )
Không dich được đề bài, đề là:
\(\dfrac{2x^2-1}{x^3+1}+\dfrac{1}{x+1}=2x\left(\dfrac{1-x^2-x}{x^2-x+1}\right)\)
Hay: \(...=2\left(1-x^2-\dfrac{x}{x^2-x+1}\right)\)
Giải các phương trình sau: x 2 - 1 ( x + 2 ) ( x - 3 ) = ( x - 1 ) x 2 - 4 ( x + 5 )
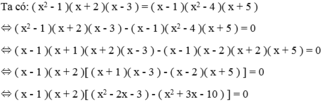
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
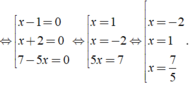
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.
\(\Leftrightarrow\left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt \(x^2+x=t\)
\(\Rightarrow t\left(t+1\right)=42\)
\(\Leftrightarrow t^2+t-42=0\Rightarrow\left[{}\begin{matrix}t=6\\t=-7\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x=6\\x^2+x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x-6=0\\x^2+x+7=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
Giải phương trình: x 2 + x ( x + 1 ) 3 = x + 1 .
A. S = 2 ; 3 2
B. S = 2 ; - 3 2
C. S = - 2 ; 3 2
D. S = - 2 ; - 3 2
1.Giải các phương trình sau:
a) 2x2 +16 -6 = 4\(\sqrt{x\left(x+8\right)}\)
b) x4 -8x2 + x-2\(\sqrt{x-1}\) + 16=0
2. Gọi x1;x2 là nghiệm phương trình x2 -3x -7 =0. Không giải phương trình tính các giá trị của biểu thức sau:
A = \(\dfrac{1}{x_1-1}+\dfrac{1}{x_2-1}\)
B= \(x^2_1+x_2^2\)
C= |x1 - x2|
D= \(x_1^4+x_2^4\)
E= (3x1 + x2) (3x2 + x1)
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
Cho phương trình ẩn x: x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2
Giải phương trình khi a = 1
Khi a = 1, ta có phương trình:
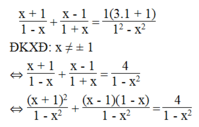
⇔ x + 1 2 + (x – 1)(1 – x) = 4
⇔ x 2 + 2x + 1 + x – x 2 – 1 + x = 4
⇔ 4x = 4 ⇔ x = 1 (loại)
Vậy phương trình vô nghiệm.