Những câu hỏi liên quan
Bài 19: Cho tam giác ABC vuông tại A (AB < AC). Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N. a/ Chứng minh tứ giác AMIN là hình chữ nhật. b/ Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi. c/ Cho AC = 20 cm, BC = 25 cm. Tính diện tích ΔABC
Cho tam giác ABC vuông tại A (ABAC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AB tại M và IN vuông góc với AC tại N a) Chứng minh tứ giác AMIN là hình chữ nhật b) Gọi D là điểm đối xứng của I qua N.Chứng minh tứ giác ADCI là hình thoi c) Cho AC20cm, BC25cm.Tính diện tích tam giác ABC d) Đường thẳng BN cắt cạnh DC tại K. chứng minh DK phần DC 1 phần 3
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AB tại M và IN vuông góc với AC tại N
a) Chứng minh tứ giác AMIN là hình chữ nhật
b) Gọi D là điểm đối xứng của I qua N.Chứng minh tứ giác ADCI là hình thoi
c) Cho AC=20cm, BC=25cm.Tính diện tích tam giác ABC
d) Đường thẳng BN cắt cạnh DC tại K. chứng minh DK phần DC = 1 phần 3
a: Xét tứ giác AMIN có
góc AMI=góc ANI=góc MAN=90 độ
nên AMIN là hình chữ nhật
b: Xét ΔABC có
I là trung điểm của BC
IN//AB
Do đó: N là trung điểm của AC
Xét tứ giác ADCI có
N là trung điểm chung của AC và DI
IA=IC
Do đó: ADCI là hình thoi
c: AB=căn(25^2-20^2)=15cm
S=15*20/2=150cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N
a, Tính AI
b, Chứng minh tứ giác AMIN là hình chữ nhật
c, Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi
a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔABC vuông tại A
mà AI là đường trung tuyến
nên \(AI=\dfrac{BC}{2}=5\left(cm\right)\)
b: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{MAN}=90^0\)
=>AMIN là hình chữ nhật
c: Xét ΔABC có
I là trung điểm của CB
IN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AICD có
N là trung điểm chung của AC và ID
=>AICD là hình bình hành
Hình bình hành AICD có AC\(\perp\)ID
nên AICD là hình thoi
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.a) Chứng minh tứ giác AMIN là hình chữ nhật.b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.c) Cho AC 20cm, BC 25cm.Tính diện tích ΔABCd) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
a: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
Do đó:AMIN là hình chữ nhật
b: Xét tứ giác ADCI có
N là trung điểm của AC
N là trung điểm của DI
Do đó: ADCI là hình bình hành
mà IA=IC
nên ADCI là hình thoi
c: AB=15cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=15\cdot10=150\left(cm^2\right)\)
Đúng 0
Bình luận (1)
Bài 5: (4 điểm) Cho tam giác ABC vuông tại A (AB AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.a) Chứng minh tứ giác AMIN là hình chữ nhật.b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.c) Cho AC 20cm, BC 25cm.Tính diện tích ΔABCd) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
Đọc tiếp
Bài 5: (4 điểm) Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
TK
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
Đúng 4
Bình luận (29)
Cho tam giác ABC vuông tại A (AB AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.a) Chứng minh tứ giác AMIN là hình chữ nhật.b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.c) Cho AC 20cm, BC 25cm.Tính diện tích ΔABCd) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
D
K
D
C
1
3
Đọc tiếp
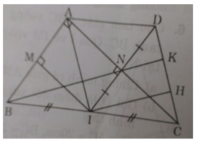
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh: D K D C = 1 3
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.a) Tứ giác AMIN là hình gì?b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.c) Tìm điều kiện của tam giác ABC để tứ giác AMIN là hình vuông . Khi đó tứ giác AICD là hình gì?d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:dfrac{DK}{DC}dfrac{1}{3}
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Tứ giác AMIN là hình gì?
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMIN là hình vuông . Khi đó tứ giác AICD là hình gì?
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:\(\dfrac{DK}{DC}\)=\(\dfrac{1}{3}\)
a: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
Do đó: AMIN là hình chữ nhật
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB < AC ) . Gọi I là trung điểm của cạnh BC . Qua I vẽ IM vuong góc vs AB tại M và IN vuông góc vs AC tại N
a) Chứng minh tứ giác AMIN là hình chứ nhật
b) Gọi D là điểm đối xứng của I qua N . CM tứ giác ACID là hình thoi
c) CHo AC = 20cm ,BC = 25cm . Tính diện tích tam giác ABC
Tứ giác AMIN có 3 góc vuông nên là HCH Tứ giác AICD có 2 đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành mà hình bình hành có 2 đường chéo vuông Nên tứ giác AICD là hình thoi (dhnb)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Tính AI.
b) Chứng minh tứ giác AMIN là hình chữ nhật.
c) Gọi D là điểm đối xứng của I qua N. chứng minh tứ giác ADCI là hình tho
a: BC=10cm
=>AI=5cm
b: Xét tứ giác AMIN có
góc AMI=góc ANI=góc MAN=90 độ
nên AMIN là hình chữ nhật
c: Xét ΔABC có
I là trung điểm của BC
IN//AB
Do đó: N là trung điểm của AC
Xét tứ giác ADCI có
N là trung điểm chung của AC và DI
IA=IC
Do đó: ADCI là hình thoi
Đúng 1
Bình luận (1)