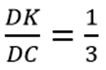Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
a: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
Do đó:AMIN là hình chữ nhật
b: Xét tứ giác ADCI có
N là trung điểm của AC
N là trung điểm của DI
Do đó: ADCI là hình bình hành
mà IA=IC
nên ADCI là hình thoi
c: AB=15cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=15\cdot10=150\left(cm^2\right)\)