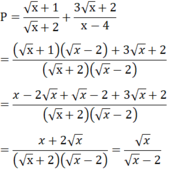Những câu hỏi liên quan
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
Cho biểu thức P= x^4+x/x^2-x+1 +1 - 2x^2+3x+1/x+1
a). Rút gọn biểu thức P
b). Tính GTNN của P
(a) Điều kiện : \(x\ne-1.\)
Ta có : \(P=\dfrac{x^4+x}{x^2-x+1}+1-\dfrac{2x^2+3x+1}{x+1}\)
\(=\dfrac{x\left(x^3+1\right)}{x^2-x+1}+1-\dfrac{\left(2x+1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x\left(x+1\right)\left(x^2-x+1\right)}{x^2-x+1}+1-\left(2x+1\right)\)
\(=x\left(x+1\right)+1-2x-1\)
\(=x^2-x.\)
Vậy : Với mọi \(x\ne-1\) thì \(P=x^2-x.\)
(b) Ta có : \(P=x^2-x\)
\(=\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]-\left(\dfrac{1}{2}\right)^2\)
\(=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Vậy : \(MinP=-\dfrac{1}{4}.\) Dấu đẳng thức xảy ra khi và chỉ khi \(x=\dfrac{1}{2}.\)
Đúng 0
Bình luận (0)
a) rút gọn biểu thức
A = 5 ( x + 1 )2 - 3 ( x -3 )2 - 4 ( x + 2 ) ( x - 2 )
b) rút gọn các biểu thức sau và tính giá trị của biểu thức tại x = -7
B = ( 2x - 3 ) ( 3x + 5 ) - 2x ( x - 2 )2 - ( 2x - 3 ) ( 2x + 3 )
`Answer:`
`a)`
`A=5(x+1)^2-3(x-3)^2-4(x^2-4)`
`=>A=5(x^2+2x+1)-3(x^2-6x+9)-4x^2+16`
`=>A=5x^2+10x+5-3x^2+18x-27-4x^2+16`
`=>A=(5x^2-3x^2-4x^2)+(10x+18x)+(5-27+16)`
`=>A=-2x^2+28x-6`
`b)`
`B=5(x+1)^2-3(x-3)^2-4(x+2)(x-2)`
`=2x(3x+5)-3(3x+5)-2x(x^2-4x+4)-[(2x)^2-3^2]`
`=6x^2+10x-9x-15-2x^3+8x^2-8x-4x^2+9`
`=(6x^2-4x^2+8x^2)-2x^3+(10x-9x-8x)+(-15+9)`
Thay `x=-7` vào ta được:
`B=10(-7)^2-2(-7)^3-7(-7)-6`
`=>B=10.49-2(-343)+49-6`
`=>B=490+686+49-6`
`=>B=1219`
Cho biểu thức \(A=\dfrac{2}{2+\sqrt{x}}+\dfrac{2\sqrt{x}}{2-\sqrt{x}}-\dfrac{2x}{4-x}\) (x ≥ 0 ; x = 4)
Rút gọn biểu thức A
\(\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}-\dfrac{2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}+4\sqrt{x}+2x-2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2}{2+\sqrt{x}}\)
Đúng 1
Bình luận (0)
Cho biểu thức: A = \(\dfrac{x+2}{2x-4}+\dfrac{x-2}{2x+4}+\dfrac{8}{x^2-4}\)
a) Với giá trị nào của x thì biểu thức được xác định.
b) Rút gọn biểu thức A.
c) Tìm giá trị của x để biểu thức A có giá trị bằng -3.
\(a,ĐK:x\ne\pm2\\ b,A=\dfrac{x^2+4x+4+x^2-4x+4+16}{2\left(x-2\right)\left(x+2\right)}\\ A=\dfrac{2x^2+32}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+16}{x^2-4}\\ c,A=-3\Leftrightarrow-3x^2+12=x^2+16\\ \Leftrightarrow4x^2=-4\Leftrightarrow x\in\varnothing\)
Đúng 1
Bình luận (0)
Cho biểu thức A= ( 1 - x^2 )( x + 5 ) -4x( 1 - x ) +( x- 2)( x^ 2 + 2x + 4)
a) Rút gọn biểu thức A
b) Tìm giá trị lớn nhất của biểu thức A
Rút gọn biểu thức rồi tìm giá trị x để biểu thức rút gọn âm:
\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}\)
\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}\)
Để biểu thức trên nhận giá trị âm khi \(\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}< 0\)
\(\Rightarrow x^3-2x^2-4x+8< 0\)do \(\left(x-2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)-2x\left(x+2\right)< 0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)^2< 0\Leftrightarrow x< -2\)
Đúng 1
Bình luận (0)
Phần tự luậnNội dung câu hỏi 1Cho biểu thức:
P
x
+
1
x
+
2
+
3
x
+
2
x
-
4
Q
x
-
5
x
+...
Đọc tiếp
Phần tự luận
Nội dung câu hỏi 1
Cho biểu thức:
P = x + 1 x + 2 + 3 x + 2 x - 4
Q = x - 5 x + 6 x + 2 x với x > 0, x khác 4
a) Rút gọn biểu thức P