Những câu hỏi liên quan
Cho hàm số bậc nhất y (2m – 1)x + m – 1, với m là tham số.a) Khi m 2, vẽ đồ thị của hàm số thu được và tính diện tích tam giác tạo bởi đồ thị và hai trục toạ độ. Gọi đường thẳng đó là (d1)b) Khi m - 1, vẽ đồ thị là đường thẳng (d2) của hàm số. Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d2).c) Chứng minh rằng khi m thay đổi thì các đường thẳng thu được luôn cùng đi quamột điểm cố định.
Đọc tiếp
Cho hàm số bậc nhất y = (2m – 1)x + m – 1, với m là tham số.
a) Khi m = 2, vẽ đồ thị của hàm số thu được và tính diện tích tam giác tạo bởi đồ thị và hai trục toạ độ. Gọi đường thẳng đó là (d1)
b) Khi m = - 1, vẽ đồ thị là đường thẳng (d2) của hàm số. Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d2).
c) Chứng minh rằng khi m thay đổi thì các đường thẳng thu được luôn cùng đi qua
một điểm cố định.
Cho hàm số y : x+2 (d)a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxyb) Gọi A,B là giao điểm của đường thẳng với 2 trục tọa độ. Xác định tọa độ của A,B và tính diện tích tam giác ABCc)Tính góc tạo bởi đường thẳng với trục
Xem chi tiết
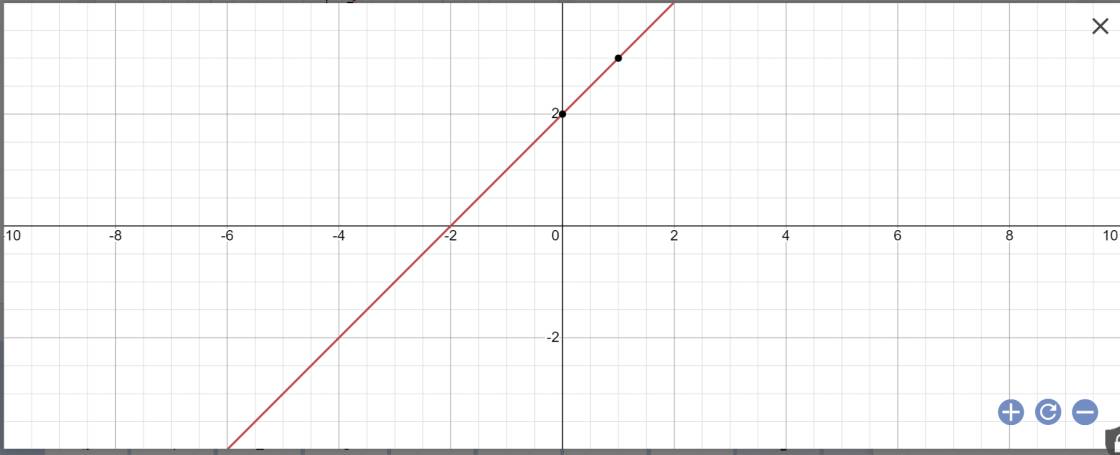
a:
b:
Sửa đề: Tính diện tích tam giác ABO
tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy: A(-2;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Vậy: B(0;2)
O(0;0) A(-2;0); B(0;2)
\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{4}=2\)
\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
Vì \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)
c: Sửa đề: Tính góc tạo bởi đường thẳng với trục ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
Đúng 0
Bình luận (0)
Cho hàm số y : x+2 (d) a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxy
b) Gọi A,B là giao điểm của đường thẳng với 2 trục tọa độ. Xác định tọa độ của A,B và tính diện tích tam giác ABC
c)Tính góc tạo bởi đường thẳng với trục
Xem chi tiết
Cho các hàm số y=2x ; y = 3x + 3 và y= -2x+5
a) Vẽ đồ thị các hàm số trên cùng một hệ trục tọa độ. Tính số đo các góc tạo bởi đồ thị các hàm số trên với trục Ox.
b) Tính diện tích các tam giác tạo bởi mỗi đường thẳng y= 3x + 3 và y= -2x+5 với 2 trục tọa độ
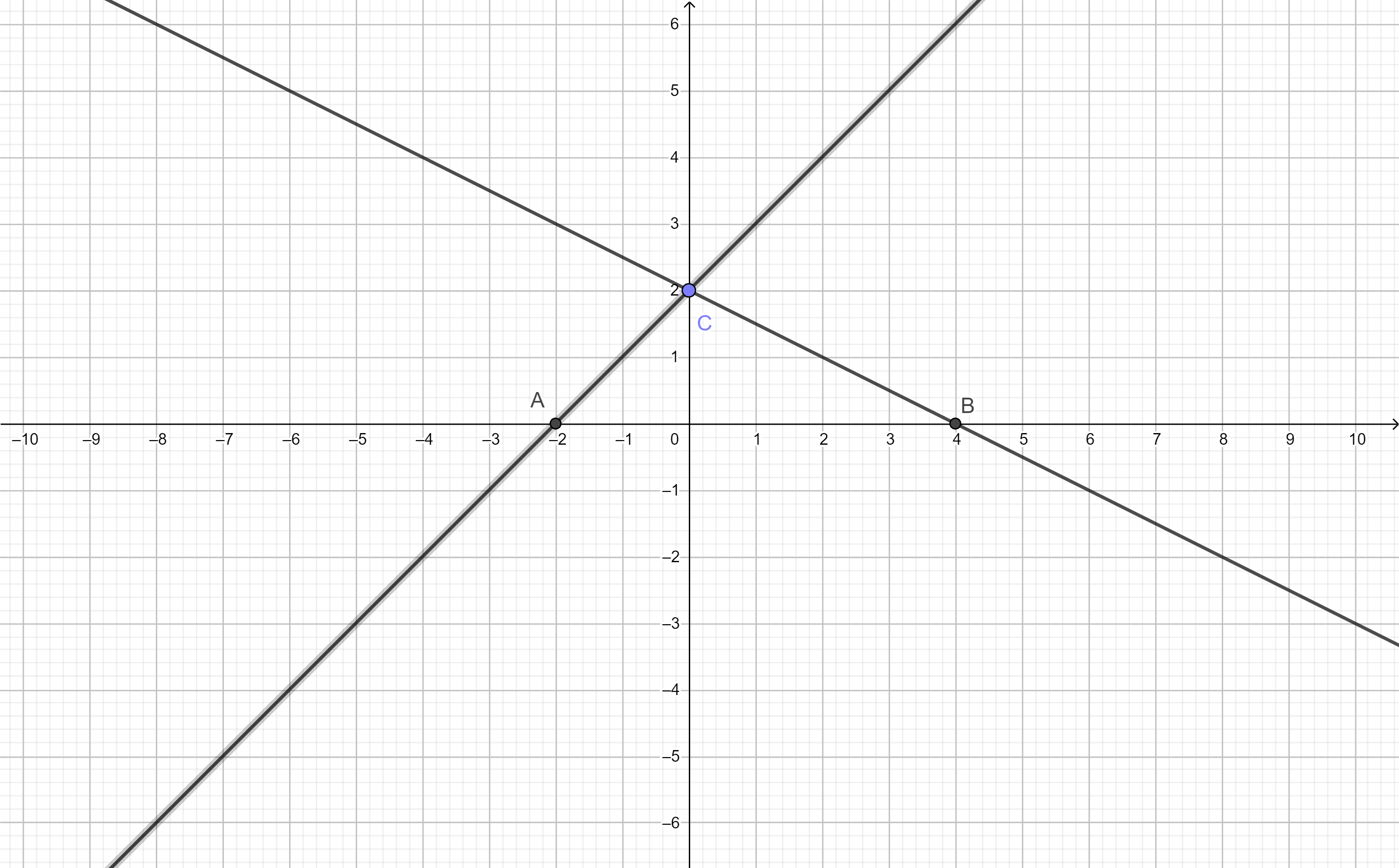
cho hàm số y=x+2 và y=-1/2x+2
a,vẽ 2 đồ thị trên cùng 1 mặt phẳng
b,gọi C là giao của 2 đường thẳng,đường thẳng y=x+2 vớitrục hoàn là A ,giao điểm của đường thẳng y=-1/2x+2 với trục hoàn là B.tính chu vi và diện tích tam giác ABC
\(b,\) PTHDGD: \(x+2=-\dfrac{1}{2}x+2\Leftrightarrow x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)
PT giao Ox của \(y=x+2:\) \(y=0\Leftrightarrow x=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)
PT giao Ox của \(y=-\dfrac{1}{2}x+2:\) \(y=0\Leftrightarrow-\dfrac{1}{2}x=-2\Leftrightarrow x=4\Leftrightarrow B\left(4;0\right)\Leftrightarrow OB=4\)
Ta có: \(\left\{{}\begin{matrix}AB=OA+OB=6\\AC=\sqrt{\left(-2\right)^2+2^2}=2\sqrt{2}\\BC=\sqrt{4^2+2^2}=2\sqrt{5}\end{matrix}\right.\)
Do đó \(P_{ABC}=AB+BC+CA=6+2\sqrt{2}+2\sqrt{5}\)
\(S_{ABC}=\dfrac{1}{2}OC\cdot AB=\dfrac{1}{2}\cdot2\cdot6=6\left(đvdt\right)\)
Đúng 0
Bình luận (0)
cho hàm số y=x 4 và y=-x 2
a,vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b,gọi A là giao điểm của hai đường thẳng trên,B và C lần lượt là giao điểm của 2 đường thẳng đó với trục Ox.Tính chu vi và diện tích của tam giác ABC
Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -
Đúng 0
Bình luận (0)
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Cho đường thẳng (d): y= (m-2)x+2m-3
a) vẽ đồ thị của hàm số khi m=1. Gọi đt đó là (d1)
b) Cho (d2): y= x-5. Tìm tọa độ giao điểm A của (d1) và (d2)
c) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy
Cho đường thẳng (d): y= (m-2)x+2m-3
a) vẽ đồ thị của hàm số khi m=1. Gọi đt đó là (d1)
b) Cho (d2): y= x-5. Tìm tọa độ giao điểm A của (d1) và (d2)
c) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy
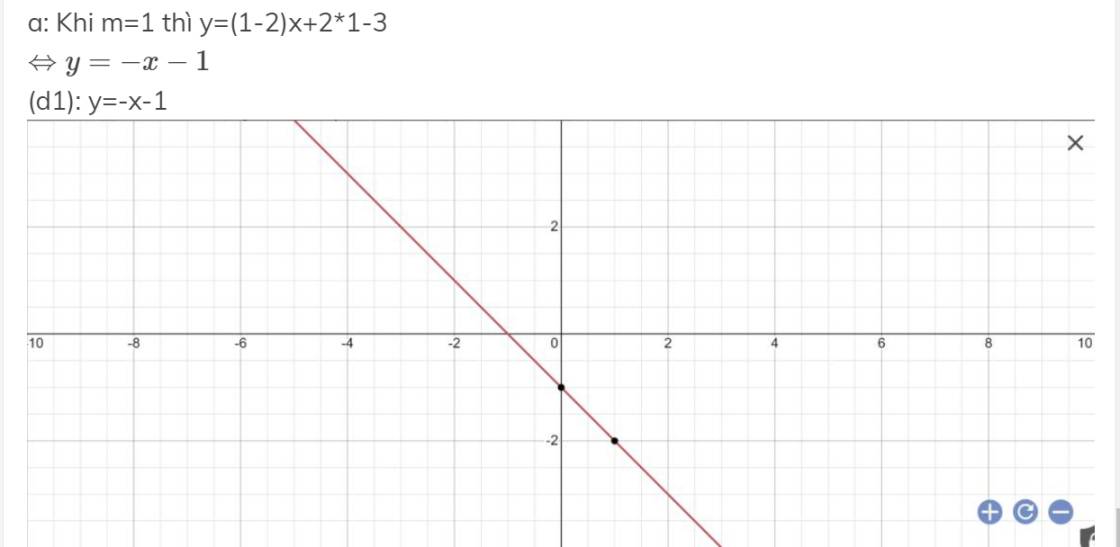
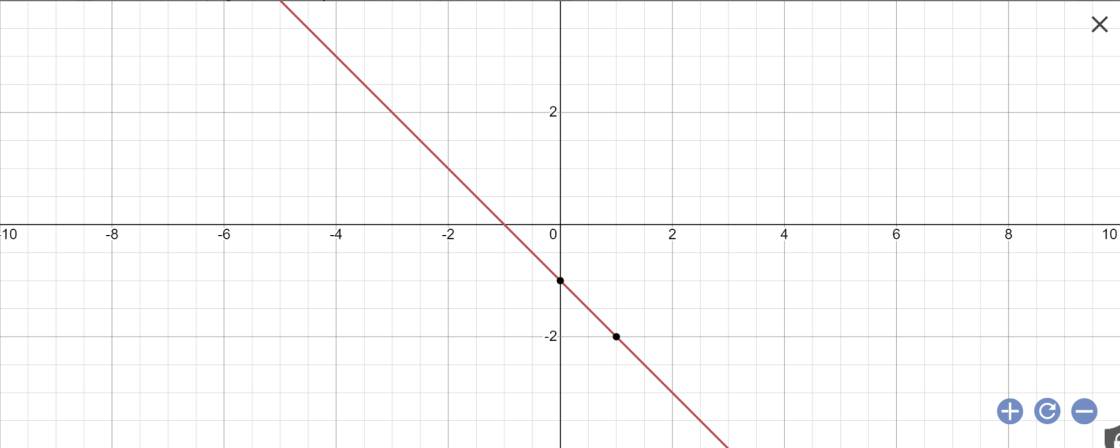
a: Khi m=1 thì y=(1-2)x+2*1-3
\(\Leftrightarrow y=-x-1\)
(d1): y=-x-1
b: Tọa độ A là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}-x-1=x-5\\y=x-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-4\\y=x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-5=-3\end{matrix}\right.\)
c: \(a_1\cdot a_2=1\cdot\left(-1\right)=-1\)
=>\(\left(d1\right)\perp\left(d2\right)\)
Đúng 1
Bình luận (0)