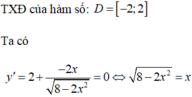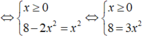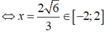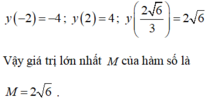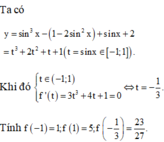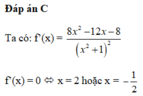Những câu hỏi liên quan
Tìm giá trị lớn nhất M của hàm số
y
2
x
+
8
-
2
x
2
trên tập xác định của nó? A.
M
2
5
B.
M
8
3
3
C.
M
2...
Đọc tiếp
Tìm giá trị lớn nhất M của hàm số y = 2 x + 8 - 2 x 2 trên tập xác định của nó?
A. M = 2 5
B. M = 8 3 3
C. M = 2 6
D. M = 4
Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó
![]()
Vế phải có nghĩa khi 1 ≤ x ≤ 5
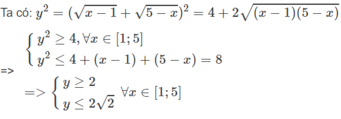
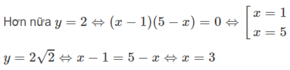
Vậy giá trị lớn nhất của hàm số đã cho bằng 2 2 khi x = 3, giá trị nhỏ nhất của hàm số đã cho bằng 2 khi x = 1 hoặc x = 5.
Đúng 0
Bình luận (0)
Giá trị lớn nhất của hàm số y = sin 3 x -cos2x+sinx+2 trên tập xác định của nó là
A. -1
B. 5
C. 3
D. 1
Giá trị lớn nhất của hàm số y = sin 3 x − cos 2 x + sin x + 2 trên tập xác định của nó là
A. -1
B. 5
C. 3
D. 1
Đáp án B.
Ta có
y = sin 3 x − 1 − 2 sin 2 x + s inx + 2 = t 3 + 2 t 2 + t + 1 t = s inx ∈ − 1 ; 1 .
Khi đó t ∈ − 1 ; 1 f ' t = 3 t 3 + 4 t + 1 = 0 ⇔ t = − 1 3 .
Tính f − 1 = 1 ; f 1 = 5 ; f − 1 3 = 23 27 .
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Đúng 0
Bình luận (0)
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Đúng 0
Bình luận (0)
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Đúng 0
Bình luận (0)
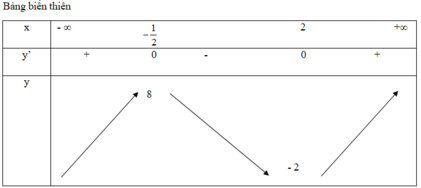
Giá trị lớn nhất của hàm số y = 6 - 8 x x 2 + 1 trên tập xác định của nó là
A. - 2
B. 2 3
C. 8
D. 10
Cho hàm số y=2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là R.
B. Tập giá trị của hàm số là (0;+∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Đúng 4
Bình luận (0)
Tìm tập xác định: y=1/căn 3 cot2x+1 Tìm giá trị lớn nhất,nhỏ nhất của hàm số: y= 4cos(2x +π/5) +9
a: ĐKXĐ: 2x<>kpi và cot2x<>-1/căn 3
=>x<>kpi/2 và 2x<>-pi/3+kpi
=>x<>kpi/2 và x<>-pi/6+kpi/2
b: -1<=cos(2x+pi/5)<=1
=>-4<=4cos(2x+pi/5)<=4
=>5<=y<=13
y=5 khi 2x+pi/5=pi+k2pi
=>x=2/5pi+kpi
y=13 khi 2x+pi/5=k2pi
=>x=kpi-pi/10
Đúng 0
Bình luận (0)