Tập nghiệm bất phương trình: l o g 0 , 5 ( x − 4 ) + 1 ≥ 0 là:
A. 4 ; 9 2
B. ( − ∞ ; 6 )
C. ( 4 ; + ∞ )
D. ( 4 ; 6 ]
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Cho hệ bất phương trình 0≤ x ≤ 4; 0 ≤ y ≤ 5; y - x ≥ 3
a. Biểu diễn tập nghiệm của hệ bất phương trình trên hệ trục Oxy
b. Tìm giá trị lớn nhất của biểu thức S= 2x + y
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - 2y + 3 \le 0\\x + 3y > - 2\\x \le 0\end{array} \right.\)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau.
Bước 1: Mở trang Geoebra
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
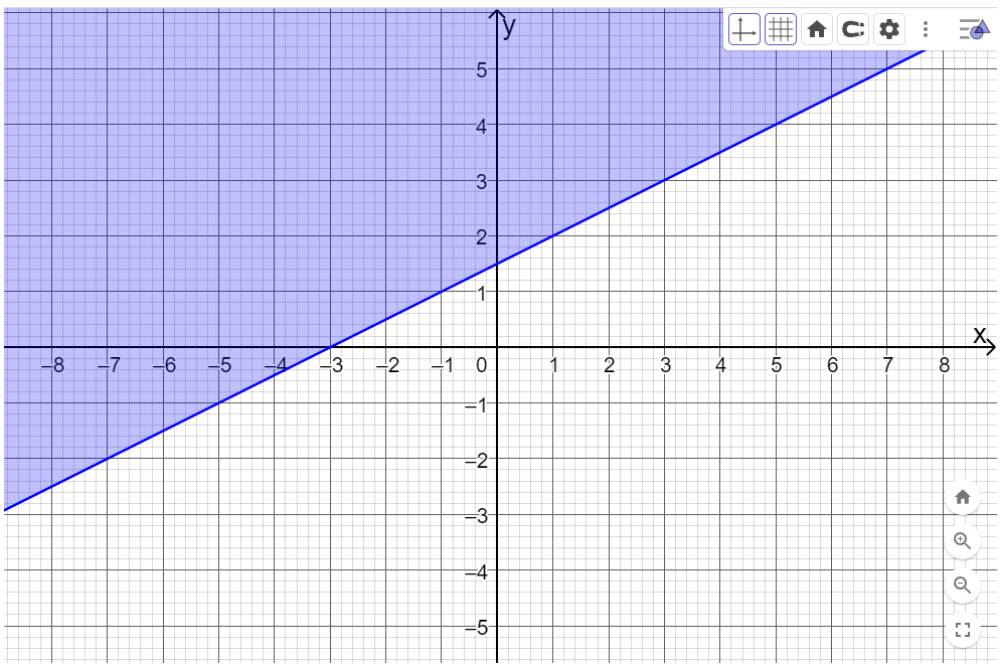
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
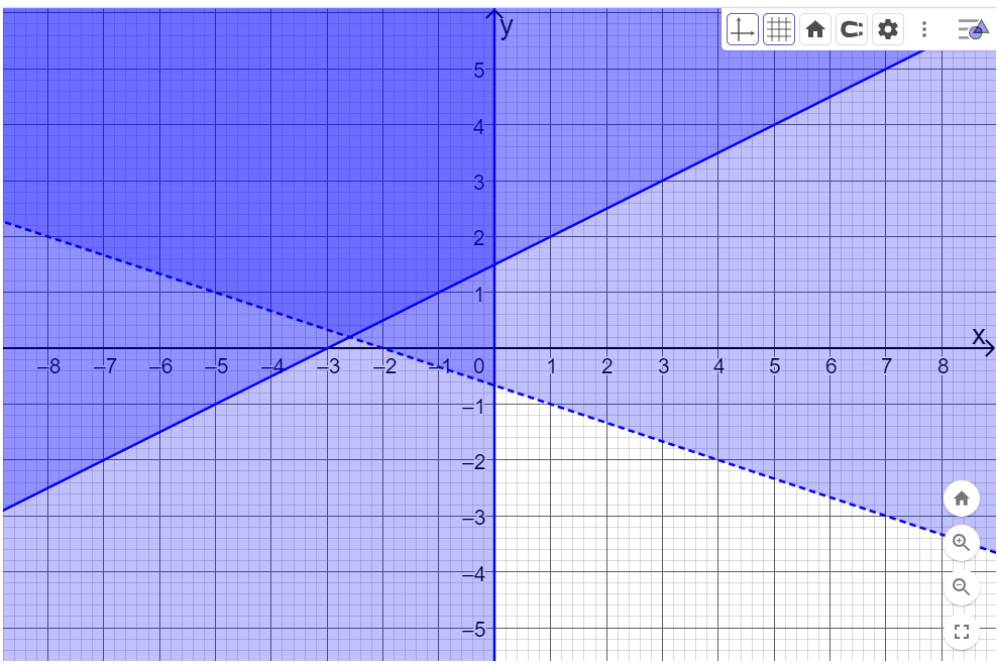
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.
Tập nghiệm của bất phương trình x - 4 x + 4 > 0
A. S = ℝ \ 2
B. S = ℝ
C. S = ℝ \ - 2
D. S = 2 ; + ∞
Ta có : x2 – 4x + 4 =(x- 2)2
Do đó,để x2 – 4x + 4 > 0
⇔
x
-
2
≠
0
⇔
x
≠
2
Tập nghiệm của bất phương trình là S = R\ {2}.
Chọn A
Tìm \(D = E \cap G\) biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:
a) \(2x + 3 \ge 0\) và \( - x + 5 \ge 0\)
b) \(x + 2 > 0\) và \(2x - 9 < 0\)
a) Ta có: \(2x + 3 \ge 0 \Leftrightarrow x \ge \frac{{ - 3}}{2}\)
\( \Rightarrow \) Tập hợp E là: \(E = \left\{ {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2}} \right\}\)
và \( - x + 5 \ge 0 \Leftrightarrow x \le 5\)
\( \Rightarrow \) Tập hợp G là \(G = \left\{ {x \in \mathbb{R}|x \le 5} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x \ge \frac{{ - 3}}{2}\) và \(x \le 5\)} \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}\)
Vậy tập hợp D \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\} = [\frac{{ - 3}}{2}; 5]\)
b) Ta có: \(x + 2 > 0 \Leftrightarrow x>-2\)
\( \Rightarrow E = \left\{ {x \in \mathbb{R}|x >-2 }\right\}\)
và \( 2x - 9 < 0 \Leftrightarrow x < \frac{9}{2}\)
\( \Rightarrow G = \left\{ {x \in \mathbb{R}|x < \frac{9}{2}} \right\}\)
\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x > -2 \) và \(x < \frac{9}{2}\)} \( = \left\{ {x \in \mathbb{R}|-2<x< {9\over 2} } \right\}\)
Vậy \( D= \left\{ {x \in \mathbb{R}|-2<x< {9\over 2}} \right\}=(-2;{9\over 2})\)
Tập nghiệm của bất phương trình x − 3 x + 4 < 0 là
A. x > 4
B. -4 < x < 3
C. x < 3
D. x ≠ -4
Tập nghiệm của bất phương trình (x² + 2x -3)(x² -4x+4) >= 0
\(\left(x^2+2x-3\right)\left(x-2\right)^2>=0\)
=>(x+3)(x-1)>=0
=>x>=1 hoặc x<=-3
Tìm tập nghiệm của bất phương trình log 2 5 ( x - 4 ) + 1 > 0 .
A. [ 13 2 ; + ∞ )
B. - ∞ ; 13 2
C. 4 ; + ∞
D. 4 ; 13 2