Số giao điểm của đường cong y = x 3 - 2 x 2 + 2 x + 1 và đường thẳng y = 1 - x bằng
A. 1
B. 2
C. 3
D. 0
Những câu hỏi liên quan
Số giao điểm của đường thẳng
y
x
+
2
và đường cong
y
x
3
+
2
là A. 1 B. 0 C. 3 D. 2
Đọc tiếp
Số giao điểm của đường thẳng y = x + 2 và đường cong y = x 3 + 2 là
A. 1
B. 0
C. 3
D. 2
Số giao điểm của đường cong y=x3-2x2+2x+1 và đường thẳng y=1-x bằng
pt hoành độ giao điểm : x 3 - 2x2 + 2x +1 = 1 -x
⇔ x = 0
Thay x=0 vào pt đường cong ⇒ y=1
⇒ giao điểm là (0;1) ⇒ có một giao điểm
Đúng 0
Bình luận (0)
Số giao điểm của đường cong y = x 3 − 2 x 3 + 2 x + 1 và đường thẳng y=1-x bằng
A.3
B.2
C.1
D.0
Đáp án C
Xét phương trình
x 3 − 2 x 2 + 2 x + 1 = 1 − x ⇔ x 3 − 2 x 2 + 3 x = 0 ⇔ x = 0 .
Bậy giao điểm của 2 đường cao là (0;1).
Đúng 0
Bình luận (0)
Số giao điểm của đường cong y = x 3 - 2 x 2 + 2 x + 1 và đường thẳng y = 1 - x bằng
A. 0
B. 2
C. 1
D. 3
Số giao điểm của đường cong
y
x
3
−
2
x
2
+
2
x
+
1
và đường thẳng
y
1
−
x
bằng A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Số giao điểm của đường cong y = x 3 − 2 x 2 + 2 x + 1 và đường thẳng y = 1 − x bằng
A. 1
B. 2
C. 3
D. 0
Đáp án A
Phương trình hoành độ giao điểm là:
x 3 − 2 x 2 + 2 x + 1 = 1 − x ⇔ x 3 − 2 x 2 + 3 x = 0
⇔ x = 0 do đó 2 đường cong có 1 giao điểm.
Đúng 0
Bình luận (0)
Số giao điểm của đường cong y = x 3 - 2 x 2 + 2 x + 1 và đường thẳng y = 1 - x là
A. 1
B. 2
C. 3
D. 4
Chọn A.
Phương trình hoành độ giao điểm của hai đường trên là:
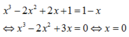
Phương trình có một nghiệm nên đường cong và đường thẳng có một giao điểm
Đúng 0
Bình luận (0)
Số giao điểm của đường cong y = x3 – 2x2 + 2x + 1 và đường thẳng y = 1 - x là
A. 1
B. 3
C. 0
D. 2
Trong mặt phẳng Oxy cho hai đường thẳng (d1): y = 3 - m(x - 2) và (d2): y = (-m + 1)x - 3. Quỹ tích giao điểm M của (d1) và (d2) là?
A. Một điểm nằm trên trục hoành.
B. Một điểm nằm trên trục tung.
C. Một đường thẳng.
D. Một đường cong dạng (P).
Giải thích.
1/ tìm tung độ giao điểm của đồ thị(C): \(\frac{2x-3}{x+3}\) và đường thẳng (d): y=x-1
2/ tiếp tuyến của đường cong(C) : y=x4+2x2 tại điểm M(1;3) có phương trình là
3/ đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số y=x3 -3x2+1 có phương trình là
1.
Pt hoành độ giao điểm: \(\frac{2x-3}{x+3}=x-1\)
\(\Leftrightarrow2x-3=x^2+2x-3\)
\(\Leftrightarrow x=0\Rightarrow y=-1\)
Vậy tung độ giao điểm là \(-1\)
2.
\(y'=4x^3+4x\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=8\\y\left(1\right)=3\end{matrix}\right.\)
Pttt: \(y=8\left(x-1\right)+3=8x-5\)
3.
\(y'=3x^2-6x\)
Lấy y chia y' và lấy phần dư ta được pt đường thẳng là: \(y=-2x+1\)