Cho các số thực a, b thỏa mãn 0 < a < 1 < b ; a b > 1 . Giá trị lớn nhất của biểu thức P = log a a b + 4 1 - log a b log a b a b bằng
A. 3.
B. -4
C. 4.
D. 2
Cho các số thực a, b thỏa mãn 0 < a < 1 < b . Tìm khẳng định đúng:
A. log a b < 0
B. ln a > ln b
C. 0 , 5 a < 0 , 5 b
D. 2 a > 2 b .
Chọn A.
Phương pháp
Xét tính đúng sai của từng đáp án dựa vào điểu kiện của a, b.
Cách giải:
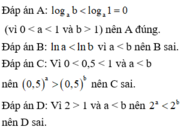
1) cho các số thực dương a,b thỏa mãn \(3a+b\le1\). Tìm Min của \(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\)
2) Với hai số thực a,b không âm thỏa mãn \(a^2+b^2=4\). Tìm Max \(M=\dfrac{ab}{a+b+2}\)
3) Cho x,y khác 0 thỏa mãn \(\left(x+y\right)xy=x^2+y^2-xy\). Tìm Max \(A=\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:
\(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8\).
Đẳng thức xảy ra khi a = b = \(\dfrac{1}{4}\).
2.
\(4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}\)
Đồng thời \(\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2\)
\(M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}\) (với \(x=a+b\Rightarrow2\le x\le2\sqrt{2}\) )
\(M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1\)
\(M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1\)
Dấu "=" xảy ra khi \(x=2\sqrt{2}\) hay \(a=b=\sqrt{2}\)
3. Chia 2 vế giả thiết cho \(x^2y^2\)
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4\)
\(A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
1. Cho các số thực không âm \(a;b;c\) (không có hai số nào đồng thời bằng 0) thỏa mãn \(a+b+c \leq 3\)
Tìm giá trị nhỏ nhất: \(A=\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\)
2. Cho các số thực \(a;b;c \in [0;1]\) thỏa mãn \(a+b+c=2\), tìm giá trị lớn nhất và nhỏ nhất của:
\(B=\dfrac{ab}{1+ab}+\dfrac{bc}{1+bc}+\dfrac{ca}{1+ca}\)
Thank you all :)
1.
Ta sẽ chứng minh BĐT sau: \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\ge\dfrac{10}{\left(a+b+c\right)^2}\)
Do vai trò a;b;c như nhau, ko mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\)
Đặt \(\left\{{}\begin{matrix}x=a+\dfrac{c}{2}\\y=b+\dfrac{c}{2}\end{matrix}\right.\) \(\Rightarrow x+y=a+b+c\)
Đồng thời \(b^2+c^2=\left(b+\dfrac{c}{2}\right)^2+\dfrac{c\left(3c-4b\right)}{4}\le\left(b+\dfrac{c}{2}\right)^2=y^2\)
Tương tự: \(a^2+c^2\le x^2\) ; \(a^2+b^2\le x^2+y^2\)
Do đó: \(A\ge\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\)
Nên ta chỉ cần chứng minh: \(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{10}{\left(x+y\right)^2}\)
Mà \(\dfrac{1}{\left(x+y\right)^2}\le\dfrac{1}{4xy}\) nên ta chỉ cần chứng minh:
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{5}{2xy}\)
\(\Leftrightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{2}{xy}+\dfrac{1}{x^2+y^2}-\dfrac{1}{2xy}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2}{x^2y^2}-\dfrac{\left(x-y\right)^2}{2xy\left(x^2+y^2\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2\left(2x^2+2y^2-xy\right)}{2x^2y^2}\ge0\) (luôn đúng)
Vậy \(A\ge\dfrac{10}{\left(a+b+c\right)^2}\ge\dfrac{10}{3^2}=\dfrac{10}{9}\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\dfrac{3}{2};\dfrac{3}{2};0\right)\) và các hoán vị của chúng
2.
Ta có: \(B=\dfrac{ab+1-1}{1+ab}+\dfrac{bc+1-1}{1+bc}+\dfrac{ca+1-1}{1+ca}\)
\(B=3-\left(\dfrac{1}{1+ab}+\dfrac{1}{1+ca}+\dfrac{1}{1+ab}\right)\)
Đặt \(C=\dfrac{1}{1+ab}+\dfrac{1}{1+bc}+\dfrac{1}{1+ca}\)
Ta có: \(C\ge\dfrac{9}{3+ab+bc+ca}\ge\dfrac{9}{3+\dfrac{1}{3}\left(a+b+c\right)^2}=\dfrac{27}{13}\)
\(\Rightarrow B\le3-\dfrac{27}{13}=\dfrac{12}{13}\)
\(B_{max}=\dfrac{12}{13}\) khi \(a=b=c=\dfrac{2}{3}\)
Do \(a;b;c\in\left[0;1\right]\)
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)\(\Leftrightarrow ab+1\ge a+b\)
\(\Leftrightarrow ab+c+1\ge a+b+c=2\)
\(\Rightarrow abc+ab+c+1\ge ab+c+1\ge2\)
\(\Rightarrow\left(c+1\right)\left(ab+1\right)\ge2\)
\(\Rightarrow\dfrac{1}{ab+1}\le\dfrac{c+1}{2}\)
Hoàn toàn tương tự, ta có:
\(\dfrac{1}{bc+1}\le\dfrac{a+1}{2}\) ; \(\dfrac{1}{ca+1}\le\dfrac{b+1}{2}\)
Cộng vế: \(C\le\dfrac{a+b+c+3}{2}=\dfrac{5}{2}\)
\(\Rightarrow B\ge3-\dfrac{5}{2}=\dfrac{1}{2}\)
\(B_{min}=\dfrac{1}{2}\) khi \(\left(a;b;c\right)=\left(0;1;1\right)\) và các hoán vị của chúng
Cho a,b là các số thực thỏa mãn 0<a<b<1. Mệnh đề nào sau đây đúng
A. log a b > 1
B. log b a < 0
C. log a b > log b a
D. log b a > log a b
Cho các số thực a , b , c > 0 và a , b , c ≠ 1 thỏa mãn log a b 2 = x , log b 2 c = y . Giá trị của log c a bằng
A. 2 x y
B. 2xy
C. 1 2 x y
D. x y 2
Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này.
Ta có ![]()

Chọn C.
Cho a,b,c,d là các số thực thỏa mãn a≥b≥c≥d>0 với a+b+c+d=1
CMR (a+2b+3c+4d)aabbccdd <1
Cho các số thực a, b thỏa mãn 0<a<b. Khẳng định nào sau đây đúng?
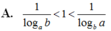
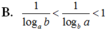
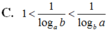
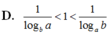
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
Cho các số thực a,b,c thỏa mãn 4a+b>8+2b và a+b+c<-1. Khi đó số nghiệm thực phân biệt của phương trình x 3 + a x 2 + b x + c = 0 bằng
A.0
B.3
C.2
D.1