Cho f x = e 1 + 1 x 2 + 1 x + 1 2 . Biết rằng f 1 . f 2 . f 3 . . . f 2017 = e m n với m, n là các số tự nhiên và m n là phân số tối giản. Tính m - n 2 .
A. m - n 2 = - 1
B. m - n 2 = 1
C. m - n 2 = 2018
D. m - n 2 = - 2018
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
. a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f( 1 2 ); f( 1 2 ). b) Cho hàm số y = g(x) = x 2 – 1. Tính g(-1); g(0
giúp e với ạ
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
giúp em mấy bài nguyên hàm với ạ. huhu
1) cho f(x)=8sin bình(x+pi/12) một nguyên hàm F(x) của f(x) thỏa F(0)=8 là
A.4x+2sin(2x+pi/6)+9
B.4x-2sin(2x+pi/6)-9
C.4x+2sin(2x+pi/6)+7
D.4x-2sin(2x+pi/6)+7
2)cho f(x)=x*(e mũ -x) một nguyên hàm F(x) của f(x) thỏa F(0)=1 là
A.-(x+1) *(e mũ -x)+1
B.-(x+1)*(e mũ -x)+2
C.(x+1)*(e mũ -x)+1
D.(x+1)*(e mũ -x)+2
Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 ; f ( e ) = 2 Tích phân ∫ 1 e f ' ( x ) ln x d x
A. 1
B. 0
C. 2
D. 3
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 , f(e) = 2. Tích phân ∫ 1 e f ' ( x ) ln x d x = ?
A. 1
B. 0
C. 2
D. 3
Đáp án A
Phương pháp: Công thức từng phần: ![]()
Cách giải:
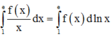
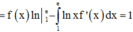
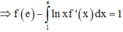
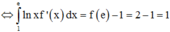
Cho hàm số \(f\left(x\right)=e^{\sqrt{x^2+1}}\left(e^x-e^{-x}\right)\). Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình \(f\left(m-7\right)+f\left(\dfrac{12}{m+1}\right)< 0\) ?
Lời giải:
Đặt $\sqrt{x^2+1}+x=a$ thì:
$f(a)=e^a-e^{\frac{1}{a}}$
$f'(a)=e^a+\frac{1}{a^2}.e^{\frac{1}{a}}>0$ với mọi $a$
Do đó hàm $f(a)$ là hàm đồng biến hay $f(x)$ là hàm đồng biến trên R
$\Rightarrow f(x)> f(0)=0$ với mọi $x>0$
$\Rightarrow f(\frac{12}{m+1})>0$ với $m$ nguyên dương
Do đó để $f(m-7)+f(\frac{12}{m+1})<0$ thì $f(m-7)<0$
$\Rightarrow m-7<0$
Mặt khác, dễ thấy: $f(x)+f(-x)=0$. Bây h xét:
$m=1$ thì $f(m-7)+f(\frac{12}{m+1})=f(-6)+f(6)=0$ (loại)
$m=2$ thì $f(m-7)+f(\frac{12}{m+1})=f(-5)+f(4)=f(4)-f(5)<0$ (chọn)
$m=3$ thì $f(m-7)+f(\frac{12}{m+1})=f(-4)+f(3)=f(3)-f(4)<0$ (chọn)
$m=4$ thì $f(m-7)+f(\frac{12}{m+1})=f(-3)+f(2,4)=f(2,4)-f(3)<0$ (chọn)
$m=5$ thì $f(m-7)+f(\frac{12}{m+1})=f(-2)+f(2)=0$ (loại)
$m=6$ thì $f(m-7)+f(\frac{12}{m+1})=f(-1)+f(12/7)>f(-1)+f(1)=0$ (loại)
Vậy có 3 số tm
Cho hàm số f(x) thỏa mãn: xf'(x).lnx + f(x) = 2x2, ∀x ∈ (1;+∞) và f(e) = e2. Tính tích phân I=\(\int\limits^{e^2}_e\dfrac{x}{f\left(x\right)}dx\)
Cách làm cơ bản của dạng này:
cho hàm số y+ f(x) + (m-1)*x (m khác 1.
a. xét công thức đã cho biết đồ thị hàm số đó đi qua điểm A(1;3)
b. tính f(-1); f(-1/2)
c. tìm x để f(x)=-5; f(x)=-4
d. vẽ đồ thị hàm số đã cho
e. trong các điểm B(-2:4) D(-1;-3); e(1/3;1) điểm nào thuộc đò thị đã cho
Câu 1: Cho x, y là các số thực lớn hơn1 sao cho \(y^x.\left(e^x\right)^{e^y}\ge x^y.(e^y)^{e^x}\). Tìm giá trị nhỏ nhất của biểu thức p = \(log_x\sqrt{xy}+log_yx\)
Câu 2 Cho hàm số y = f(x) xác định trên R\{1} có đọa hàm y' = \(\frac{1}{x-1}\), Biết f(0) = 2018, f(2) =2019. Tính S= f(3) - f(-1)?
Câu 1:
Lấy logarit cơ số tự nhiên 2 vế:
\(x.lny+e^y.x\ge y.lnx+y.e^x\)
\(\Leftrightarrow\frac{lny+e^y}{y}\ge\frac{lnx+e^x}{x}\)
Xét hàm \(f\left(t\right)=\frac{lnt+e^t}{t}\) với \(t>1\)
\(f'\left(t\right)=\frac{\left(e^t+\frac{1}{t}\right).t-lnt-e^t}{t^2}=\frac{t.e^t+1-e^t-lnt}{t^2}\)
Xét \(g\left(t\right)=t.e^t+1-e^t-lnt\Rightarrow g'\left(t\right)=e^t+t.e^t-e^t-\frac{1}{t}\)
\(g'\left(t\right)=t.e^t-\frac{1}{t}=\frac{t^2.e^t-1}{t}>0\) \(\forall t>1\)
\(\Rightarrow g\left(t\right)\) đồng biến \(\Rightarrow g\left(t\right)>g\left(1\right)=1>0\) \(\forall t>1\)
\(\Rightarrow f'\left(t\right)=\frac{g\left(t\right)}{t^2}>0\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t_1\right)\ge f\left(t_2\right)\Leftrightarrow t_1\ge t_2\)
\(\Rightarrow f\left(y\right)\ge f\left(x\right)\Leftrightarrow y\ge x\) \(\Rightarrow log_xy\ge1>0\)
\(P=log_x\left(xy\right)^{\frac{1}{2}}+log_yx=\frac{1}{2}\left(1+log_xy\right)+\frac{1}{log_xy}\)
\(P=\frac{1}{2}+\frac{1}{2}log_xy+\frac{1}{log_xy}\ge\frac{1}{2}+2\sqrt{\frac{log_xy}{2log_xy}}=\frac{1}{2}+\sqrt{2}\)
\(f'\left(x\right)=\frac{1}{x-1}\Rightarrow\int f'\left(x\right)dx=\int\frac{1}{x-1}dx\)
\(\Rightarrow f\left(x\right)=ln\left|x-1\right|+C\)
\(\Rightarrow f\left(x\right)=\left\{{}\begin{matrix}ln\left|x-1\right|+C_1\left(x>1\right)\\ln\left|x-1\right|+C_2\left(x< 1\right)\end{matrix}\right.\)
\(f\left(0\right)=2018\Leftrightarrow2018=ln\left|0-1\right|+C_2\Rightarrow C_2=2018\)
\(f\left(2\right)=2019\Rightarrow2019=ln\left|2-1\right|+C_1\Rightarrow C_1=2019\)
\(\Rightarrow f\left(x\right)=\left\{{}\begin{matrix}ln\left|x-1\right|+2019\left(x>1\right)\\ln\left|x-1\right|+2018\left(x< 1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=2019+ln2\\f\left(-1\right)=2018+ln2\end{matrix}\right.\) \(\Rightarrow S=1\)