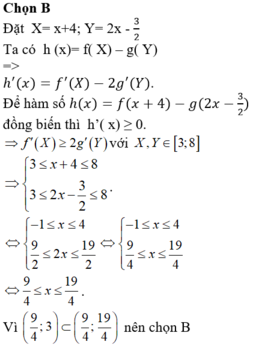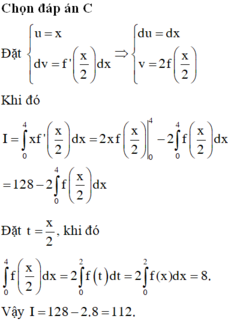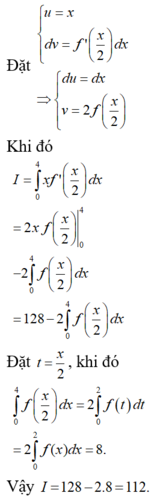Hai hàm số y = x + 4 và y = x 2 - 16 x - 4 có chung một tập xác định hay không ?

Những câu hỏi liên quan
Hai hàm số \(y=x+4\) và \(y=\dfrac{x^2-16}{x-4}\) có chung một tập xác định hay không ?
Hàm số \(y=x+4\) có tập xác đinh là \(R\); hàm số \(y=\dfrac{x^2-16}{x-4}\) có tập xác đinh là \(R\backslash\left\{4\right\}\) nên hai hàm số này không cùng tập xác định.
Đúng 0
Bình luận (0)
Cho hai số x;y ( 0 > x > y ) .Biết x/2 = y/4 và x^4 . y^4 =16 . Tìm hai số x và y đó
Cho hàm số y f(x) có đồ thị của hàm số y f (x) được cho như hình bên và các mệnh đề sau: (1). Hàm số y f(x) đồng biến trên khoảng (-1;0) (2). Hàm số y f(x) nghịch biến trên khoảng (1;2) (3). Hàm số y f(x) đồng biến trên khoảng (3;5) (4). Hàm số y f(x) có hai điểm cực đại và một điểm cực tiểu.Số mệnh đề đúng là A. 1 B. 3 C. 4 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: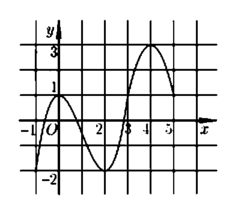
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
Đúng 0
Bình luận (0)
Cho hai hàm số y f(x) và y g(x) . Hai hàm số y f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y g’(x). Hàm số h(x)f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây? A. . B. . C. . D. .
Đọc tiếp
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
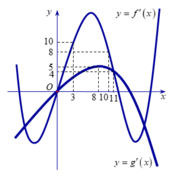
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Vẽ đồ thị của hai hàm số
y
1
4
x
2
và
y
-
1
4
x
4
trên cùng một hệ trục tọa độ.Đường thẳng đi qua B(0; 4) và song song với trục Ox có dạng : y 4 .Xét phương trình hoành độ giao điểm:
1
4
x
2
4
⇔
x
2...
Đọc tiếp
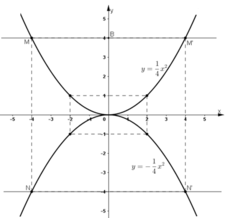
Vẽ đồ thị của hai hàm số y = 1 4 x 2 và y = - 1 4 x 4 trên cùng một hệ trục tọa độ.
Đường thẳng đi qua B(0; 4) và song song với trục Ox có dạng : y =4 .
Xét phương trình hoành độ giao điểm:
1 4 x 2 = 4 ⇔ x 2 = 16 ⇔ x = ± 4
Vậy hoành độ của M là x=-4 và M’ là x =4
- Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
 |
4 | 1 | 0 | 1 | 4 |
 |
-4 | -1 | 0 | -1 | -4 |
- Vẽ đồ thị:
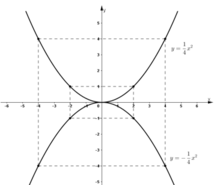
Đường thẳng qua B(0; 4) song song với Ox cắt đồ thị tại hai điểm M, M' (xem hình). Từ đồ thị ta có hoành độ của M là x = 4, của M' là x = - 4.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
liên tục trên R và
f
(
2
)
16
,
∫
0
2
f
(
x
)
d
x
4.
Tính
I
∫
0
4
x...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và f ( 2 ) = 16 , ∫ 0 2 f ( x ) d x = 4. Tính I = ∫ 0 4 x f ' x 2 d x .
A. I = 144
B. I = 12
C. I = 112
D. I = 28
:Cho hai hàm số bậc nhất y ( m - 2 )x +7 và y= (2m -5 )x -8,đô thị của hai hàm số là hai đường thẳng song song khi m bằng : A. -3 B.-4 C.3 D.4
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hàm số \(y = f\left( x \right) + g\left( x \right)\) có liên tục tại \(x = 2\) không? Giải thích.
Đặt \(h\left( x \right) = f\left( x \right) + g\left( x \right) = \frac{1}{{x - 1}} + \sqrt {4 - x} \). Ta có:
\(\begin{array}{l}h\left( 2 \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \\\mathop {\lim }\limits_{x \to 2} h\left( x \right) = \mathop {\lim }\limits_{x \to x} \left( {\frac{1}{{x - 1}} + \sqrt {4 - x} } \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 2} h\left( x \right) = h\left( 2 \right)\) nên hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \(x = 2\).
Đúng 0
Bình luận (0)
Hàm số nào sau đây là hàm số bậc hai?
a) \(y = 9{x^2} + 5x + 4\)
b) \(y = 3{x^3} + 2x + 1\)
c) \(y = - 4{(x + 2)^3} + 2(2{x^3} + 1) + x + 4\)
d) \(y = 5{x^2} + \sqrt x + 2\)
Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
liên tục trên R và
f
(
2
)
16
,
∫
0
2
f
(
x
)
d
x
4
Tính
I
∫
0
4
x
f
(
x
2
)
d...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và f ( 2 ) = 16 , ∫ 0 2 f ( x ) d x = 4 Tính I = ∫ 0 4 x f ' ( x 2 ) d x
![]()
![]()
![]()
![]()