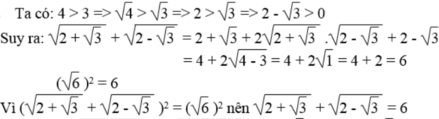Chứng minh các đẳng thức sau: 3 2 6 + 2 2 3 - 4 3 2 = 6 6

Những câu hỏi liên quan
Chứng minh các đẳng thức sau:
\(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
Chứng minh các đẳng thức: 2 + 3 + 2 - 3 = 6
Chứng minh các đẳng thức sau:
e) \(\left(\dfrac{3}{2}.\sqrt{6}+2.\sqrt{\dfrac{2}{3}}-4.\sqrt{\dfrac{3}{2}}\right).\left(\dfrac{3}{2}.\sqrt{6}+2.\sqrt{\dfrac{2}{3}}+4.\sqrt{\dfrac{3}{2}}\right)=-\sqrt{2}\)
`e)(3/2sqrt6+2sqrt{2/3}-4sqrt{3/2})(3/2sqrt6+2sqrt{2/3}+4sqrt{3/2})`
`=(3/2sqrt6+2sqrt{2/3})^2-(4\sqrt{3/2})^2`
`=((3sqrt6)/2+(2sqrt2)/3)^2-16*3/2`
`=((9sqrt6)/6+(4sqrt6)/6)^2-24`
`=((13sqrt6)/6)^2-24`
`=13^2/6-24`
`=25/6`
Đúng 0
Bình luận (0)
Chứng minh đẳng thức sau:
3/2 ^6 + 2 ^2/3 4 ^3/2 = ^6 trên 6
Giúp tui nka m.n. Mai kiểm tra 1 tiết òi
Bài 1: Tìm điều kiện để các phân thức sau có ý nghĩa
a)5x-3/2x^2-x b)x^2-5x+6/x^2-1
c)2/(x+1)(x-3) d)2x+1/x^2-5x+6
Bài 2: Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
a)x-2/-x=2^3-x^3/x(x^2+2x+4) (với x =/0)
b)3x/x+y=-3x(x+y)/y^2-x^2 (với x=/ +_ y)
c)x+y/3a=3a(x+y^2)/9a^2(x+y) (với a=/ 0,x=/-y)
Bài 1:
c: ĐKXĐ: \(x\notin\left\{-1;3\right\}\)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức sau:
\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}=\sqrt{2}-1\)
giả sử 2 vế bằng nhau, nhân tích chéo, rồi được 2 vế = nhau là kết luận thỏa mãn
Đúng 0
Bình luận (0)
\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}=\frac{1}{1+\sqrt{2}}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1=vp\)
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau
a) \(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
b)\(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}=2\frac{1}{3}\)
các bạn giúp mình với
a) Biến đổi vế trái ta có:
\(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}\)
\(=\frac{3\sqrt{6}}{2}+\frac{2\sqrt{6}}{3}-\frac{4\sqrt{6}}{2}=\frac{9\sqrt{6}+4\sqrt{6}-12\sqrt{6}}{6}=\frac{\sqrt{6}}{6}=VP\)
Vậy đẳng thức trên đc chứng minh
b) Biến đổi vế trái ta có:
\(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}\)
\(=\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right)\cdot\frac{1}{\sqrt{6x}}\)
\(=x\sqrt{\frac{6}{x}\cdot\frac{1}{6x}}+\sqrt{\frac{2x}{3}\cdot\frac{1}{6x}}+\sqrt{6x}\cdot\frac{1}{\sqrt{6x}}\)
\(=x\sqrt{\frac{1}{x^2}}+\sqrt{\frac{1}{9}}+1=1+\frac{1}{3}+1=2\frac{1}{3}=VP\)
Vậy đẳng thức trên đc chứng minh
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau:
14
-
7
1
-
2
+
15
-
5
1
-...
Đọc tiếp
Chứng minh các đẳng thức sau: 14 - 7 1 - 2 + 15 - 5 1 - 3 : 1 7 - 5 = - 2
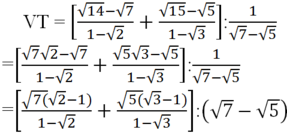
= (-√7 - √5)(√7 - √5)
= -(√7 + √5)(√7 - √5)
= -(7 - 5) = -2 = VP (đpcm)
Đúng 0
Bình luận (0)
Từ đẳng thức 2 x 3 = 1 ×6 ta có thể lập đc các cặp phân số bằng nhau như sau:2/1=6/3;. 3/1=6/2. 1/2=6/3:. 1/3=2/6. Hãy lập các cặp phân số bằng nhau từ đẳng thức 3×4=6×2
Lời giải:
$\frac{3}{6}=\frac{2}{4}$
$\frac{6}{3}=\frac{4}{2}$
$\frac{3}{2}=\frac{6}{4}$
$\frac{2}{3}=\frac{4}{6}$
Đúng 5
Bình luận (0)
Các cặp phân số bằng nhau từ đẳng thức \(3\times4=6\times2\) là:
\(\dfrac{3}{6}=\dfrac{2}{4};\) \(\dfrac{4}{6}=\dfrac{2}{3};\) \(\dfrac{6}{3}=\dfrac{2}{4};\) \(\dfrac{6}{4}=\dfrac{3}{2}\)
Đúng 5
Bình luận (0)
Chứng minh các đẳng thức sau:
a) \(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
b) \(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2X}{3}}+\sqrt{6X}\right):\sqrt{6X}=2\frac{1}{3}\)với x > 0
\(a)\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
Biến đổi vế trái , ta có :
\(VT=\frac{3}{2}\sqrt{6}+\frac{2}{3}\sqrt{3^2.\frac{2}{3}}-2\sqrt{2^2.\frac{3}{2}}\)
\(=\frac{3}{2}\sqrt{6}+\frac{2}{3}\sqrt{6}-2\sqrt{6}\)
\(=\left(\frac{3}{2}+\frac{2}{3}-2\right)\sqrt{6}\)
\(=\frac{1}{6}\sqrt{6}=\frac{\sqrt{6}}{6}=VP\left(đpcm\right)\)
\(b)\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}=2\frac{1}{3}\)
Biến đổi vế trái , ta có :
\(VT=\left(\sqrt{x^2.\frac{6}{x}}+\sqrt{\frac{6x}{3^2}}+\sqrt{6x}\right):\sqrt{6x}\)
\(=\left(\sqrt{6x}+\frac{1}{3}\sqrt{6x}+\sqrt{6x}\right):\sqrt{6x}\)
\(=\frac{7}{3}\sqrt{6x}:\sqrt{6x}\)
\(=\frac{7}{3}=2\frac{1}{3}=VP\)với x > 0 ( đpcm )