Biết ba số ln 2 ; ln 2 x − 1 ; ln 2 x + 3 lập thành một cấp số cộng. Hỏi x có giá trị gần số nào nhất trong các số sau?
A. 3
B. 2
C. 2,5
D. 3,5
Biết ba số ln 2 ; ln ( 2 x - 1 ) ; ln ( 2 x + 3 ) lập thành một cấp số cộng. Hỏi x có giá trị gần số nào nhất trong các số sau?
A. 3
B. 2
C. 2,5
D. 3,5
Chọn C
3 số : ln 2 ; ln ( 2 x - 1 ) ; ln ( 2 x + 3 ) lập thành cấp số cộng
⇒ 2 x = 2 + 11 ⇒ x ≈ 25
Tìm xđể ba số l n 2 ; l n ( 2 x - 1 ) ; l n ( 2 x + 3 ) theo thứ tự lập thành một cấp số cộng
A. 1
B. 2
C. log 2 5
D. log 2 3
Tìm x để ba số ln2; ln( 2x - 1); ln( 2x + 3) theo thứ tự lập thành cấp số cộng.
A. 1
B. 2
C. log25
D. log23
Chọn C.
Để ba số ln2; ln( 2x - 1); ln( 2x + 3) theo thứ tự lập thành cấp số cộng thì 2.ln( 2x - 1) = ln2 + ln( 2x + 3)
Suy ra: ( 2x -1) 2 = 2( 2x + 3)
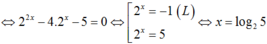
Tìm 2 số tự nhiên và a và b biết : BCNN ( a,b) = 336 và ƯC LN ( a,b) = 12
Ta co : BCNN(a;b). UCLN)a;b)=a.b=12.336=4032
Vi UCLN(a;b)=12
Dat a 12x: b=12.y voi UCLN(x;y)=1 ma a.b =4032 hay 12x.12y =4032
144.(x.y)=4032
Suy ra :x.y=28
Cap so nguyen to cung nhau co tich bang la : (28;1) va (7;4)
khi : x=28;y=1 thi a=336 va b=12
khi x=7 ; y=4 thi a=84 va b=48
**** nhe
Tìm đạo hàm của các hàm số sau:
1, \(y=3^{(\dfrac{x}{\ln(x)})}\)
2, \(y=\dfrac{1}{2}tan^2(x)+\ln(tan(x))\)
3, \(y=\sqrt[3]{ln^2(2x)}\)
1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)
Số nghiệm của phương trình ln x + ln(3x – 2) = 0 là?
A. 1.
B. 3.
C. 0.
D. 2.
Đáp án A.
Ta có ln [x(3x – 2)] = 0 <=> x(3x – 2) = 1 => x = 1 x > 3 2 .
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1
Cho hàm số f ( x ) = ln 1 - 4 ( 2 x - 1 ) 2 . Biết rằng ,f(2) + f(3) + ....+f(2020) = ln a b trong đó a b , là phân số tối giản, a, b ∈ ℕ * . Tính b - 3a
A. -2
B. 3
C. -1
D. 1
Chọn A
Ta có
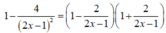
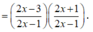
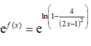
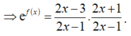
Vì f(2) + f(3) + ....+f(2020) = ln
a
b
nên 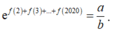
Mà ![]()
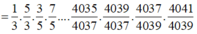
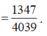
Do đó 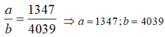
=> b = 3a = -2
Cho hàm số f ( x ) = ln ( e x + m ) có f'(ln 2) = 3.Giá trị của m bằng
A.![]()
B.![]()
C.![]()
D.![]()
Tính đạo hàm của các hàm số sau:
g) \(y = \ln (x^2+x+1)\)
l) \(y = \dfrac{\ln x}{x+1}\)
g: \(y=ln\left(x^2+x+1\right)\)
=>\(y'=\dfrac{\left(x^2+x+1\right)'}{x^2+x+1}=\dfrac{2x+1}{x^2+x+1}\)
l: \(y=\dfrac{lnx}{x+1}\)
=>\(y'=\dfrac{\left(lnx\right)'\cdot\left(x+1\right)-\left(x+1\right)'\left(lnx\right)}{\left(x+1\right)^2}\)
=>\(y'=\dfrac{\dfrac{1}{x}\left(x+1\right)-lnx}{\left(x+1\right)^2}\)
\(\Leftrightarrow y'=\dfrac{\dfrac{\left(x+1\right)}{x}-lnx}{\left(x+1\right)^2}\)