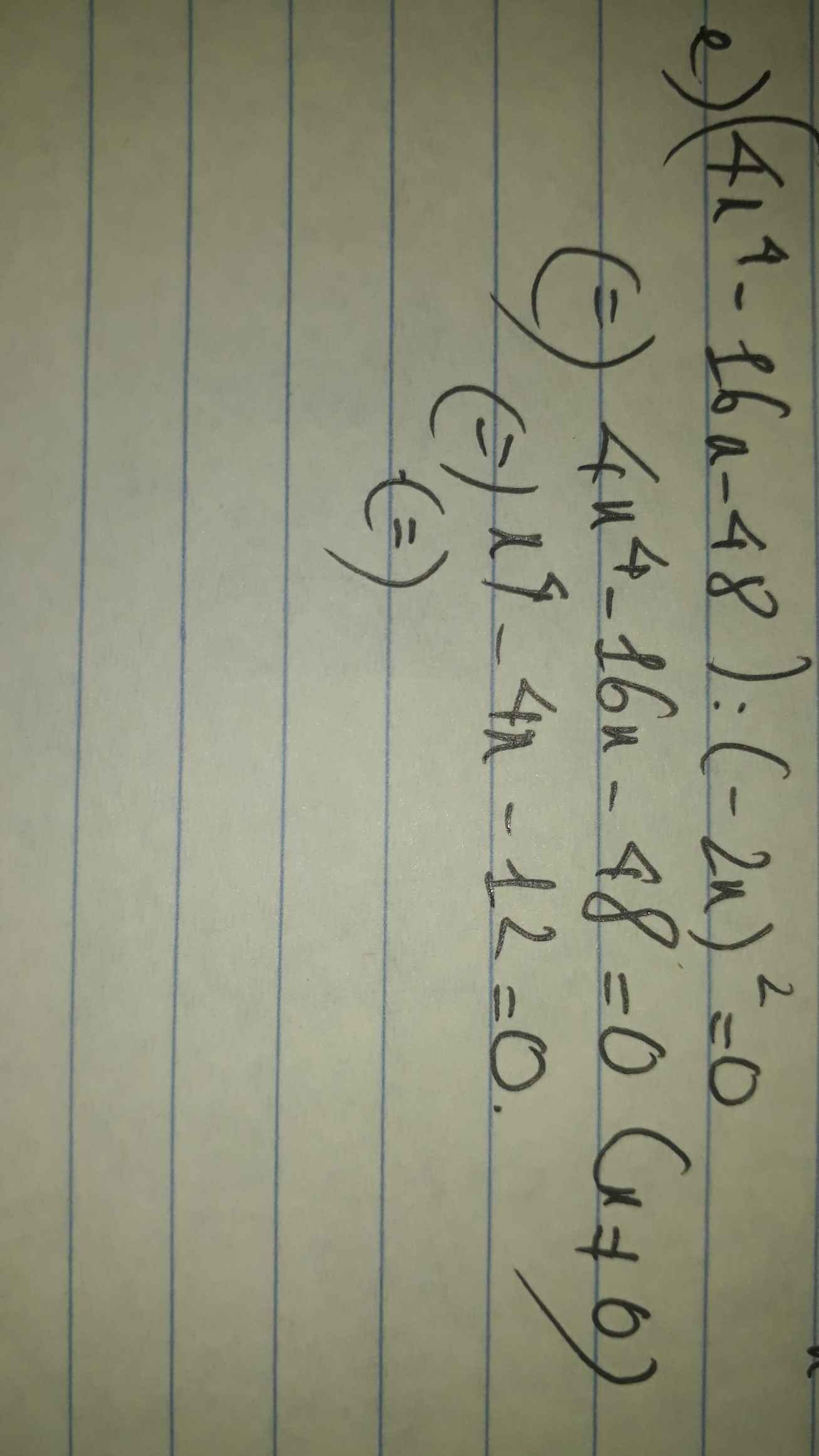1, x(x - 5) - 4x + 20 = 0

=> x(x - 5) - 4(x - 5) = 0

=> (x - 4)(x - 5) = 0

=> x - 4 = 0 hoặc x - 5 = 0

=> x = 4 hoặc x = 5

=> x thuộc {4; 5}

2, 3(x + 1) + x(x + 1) 

= (3 + x)(x + 1)

3, 2x³ + x = 0

=> x(2x² + 1) = 0

=> x = 0 hoặc 2x² + 1 = 0

=> x = 0 hoặc 2x² = -1

=> x = 0 hoặc x² = -1/2 (vô lí vì x² > hoặc = 0 với mọi x)

=> x = 0

4, x³ - 16x = 0

=> x(x² - 16) = 0

=> x = 0 hoặc x² - 16 = 0

=> x = 0 hoặc x² = 16

=> x = 0 hoặc x = 4 hoặc x = -4

=> x thuộc {-4; 0; 4}

5, x² + 6x = -9

=> x² + 6x + 9 = 0

=> x² + 2.3.x + 3² = 0

=> (x + 3)² = 0

=> x + 3 = 0

=> x = -3

6, x⁴ - 2x³ + 10x² - 20x = 0

=> x²(x² + 10) - 2x(x² + 10) = 0

=> (x² + 2x)(x² + 10) = 0

=> x(x +2)(x² + 10) = 0

-TH1: x = 0

-TH2: x + 2 = 0 => x = -2

-TH3: x² + 10 = 0 => x² = -10 (vô lí vì x² > hoặc = 0 với mọi x)

=> x thuộc {0; -2}

7, (2x - 3)² = (x + 5)²

-TH1: 2x - 3 = x + 5

=> x = 8

- TH2: - 2x + 3 = x + 5

=> -3x = 2

=> x = \(\frac{-2}{3}\)

- TH3: 2x - 3 = - x - 5

=> 3x = -2

=> x = \(\frac{-2}{3}\)

- TH4: - 2x + 3 = - x - 5

=> -x = -8

=> x = 8`

=> x thuộc {\(\frac{-2}{3}\); 8}

a) (2x + 5)(x - 3) = (x - 4)(3 - x)

<=> (2x + 5)(x - 3) + (x - 3)(x - 4) = 0

<=> (2x + 5 + x - 4)(x - 3) = 0

<=> (3x + 1)(x - 3) = 0

<=> \(\left[{}\begin{matrix}3x+1=0\\x-3=0\end{matrix}\right.\)

<=> \(\left[{}\begin{matrix}x=-\frac{1}{3}\\x=3\end{matrix}\right.\)

Vậy S = {-1/3; 3}

b) 18x²(x + 4) - 12(x² + 4x) = 0

<=> 18x²(x + 4) - 12x(x + 4) = 0

<=> 6x(x + 4)(3x - 2) = 0

<=> \(\left[{}\begin{matrix}x=0\\x+4=0\\3x-2=0\end{matrix}\right.\)

<=> \(\left[{}\begin{matrix}x=0\\x=-4\\x=\frac{2}{3}\end{matrix}\right.\)

Vậy S = {0; -2; 2/3}

\(o,x^2-9x+20=0\)

\(\Leftrightarrow x^2-4x-5x+20=0\)

\(\Leftrightarrow x\left(x-4\right)-5\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-5\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x-5=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=5\end{cases}}\)

\(n,3x^3-3x^2-6x=0\)

\(\Leftrightarrow3x\left(x^2-x-2\right)=0\)

\(\Leftrightarrow3x\left(x^2+x-2x-2\right)=0\)

\(\Leftrightarrow3x\left[x\left(x+1\right)-2\left(x+1\right)\right]=0\)

\(\Leftrightarrow3x\left(x+1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\orbr{\begin{cases}3x=0\\x+1=0\end{cases}}\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\orbr{\begin{cases}x=0\\x=-1\end{cases}}\\x=2\end{cases}}\)

\(m,x^2-11x+28=0\)

\(\Leftrightarrow x^2-4x-7x+28=0\)

\(\Leftrightarrow x\left(x-4\right)-7\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-7\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x-7=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=7\end{cases}}\)

\(l,\left(4x+3\right)^2=4\left(x^2-2x+1\right)\)

\(\Leftrightarrow16x^2+24x+9=4x^2-8x+4\)

\(\Leftrightarrow16x^2+24x+9-4x^2+8x-4=0\)

\(\Leftrightarrow12x^2+32x+5=0\)

\(\Leftrightarrow\left(x+\frac{1}{6}\right)\left(x+\frac{5}{2}\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+\frac{1}{6}=0\\x+\frac{5}{2}=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{1}{6}\\x=-\frac{5}{2}\end{cases}}\)

a: Ta có: \(x\left(2-x\right)+\left(x^2+x\right)=7\)

\(\Leftrightarrow2x-x^2+x^2+x=7\)

\(\Leftrightarrow3x=7\)

hay \(x=\dfrac{7}{3}\)

b: Ta có: \(\left(2x+1\right)^2-x\left(4-5x\right)=17\)

\(\Leftrightarrow4x^2+4x+1-4x+5x^2=17\)

\(\Leftrightarrow9x^2=16\)

\(\Leftrightarrow x^2=\dfrac{16}{9}\)

hay \(x\in\left\{\dfrac{4}{3};-\dfrac{4}{3}\right\}\)

c: Ta có: \(\left(x-4\right)^2-\left(2x+1\right)^2=0\)

\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

d: ta có: \(\dfrac{2x^3-8x^2+10x}{2x}=0\)

\(\Leftrightarrow x^2-4x+5=0\)

\(\Leftrightarrow\left(x-2\right)^2+1=0\)(vô lý)

1. \(x^3-6x^2+10x-4=0\)

<=> \(\left(x^3-2x^2\right)-\left(4x^2-8x\right)+\left(2x-4\right)=0\)

<=>  \(\left(x-2\right)\left(x^2-4x+2\right)=0\)

<=> \(\orbr{\begin{cases}x=2\\x^2-4x+2=0\left(1\right)\end{cases}}\)

Giải pt (1): \(\Delta=\left(-4\right)^2-4.2=8>0\)

=> pt (1) có 2 nghiệm: \(x_1=\frac{4+\sqrt{8}}{2}=2+\sqrt{2}\)

\(x_2=\frac{4-\sqrt{8}}{2}=2-\sqrt{2}\)

1) Ta có: \(x^3-6x^2+10x-4=0\)

       \(\Leftrightarrow\left(x^3-2x^2\right)-\left(4x^2-8x\right)+\left(2x-4\right)=0\)

       \(\Leftrightarrow x^2\left(x-2\right)-4x\left(x-2\right)+2\left(x-2\right)=0\)

       \(\Leftrightarrow\left(x^2-4x+2\right)\left(x-2\right)=0\)

   + \(x-2=0\)\(\Leftrightarrow\)\(x=2\)\(\left(TM\right)\)

   + \(x^2-4x+2=0\)\(\Leftrightarrow\)\(\left(x^2-4x+4\right)-2=0\)

                                             \(\Leftrightarrow\)\(\left(x-2\right)^2=2\)

                                             \(\Leftrightarrow\)\(x-2=\pm\sqrt{2}\)

                                             \(\Leftrightarrow\)\(\orbr{\begin{cases}x=2+\sqrt{2}\approx3,4142\left(TM\right)\\x=2-\sqrt{2}\approx0,5858\left(TM\right)\end{cases}}\)

Vậy \(S=\left\{0,5858;2;3,4142\right\}\)

4) \(x^4+5x^3-12x^2+5x+1=0\)

<=> \(\left(x^4-x^3\right)+\left(6x^3-6x^2\right)-\left(6x^2-6x\right)-\left(x-1\right)=0\) 

<=> \(\left(x^3+6x^2-6x-1\right)\left(x-1\right)=0\)

<=> \(\left[\left(x-1\right)\left(x^2+x+1\right)-6x\left(x-1\right)\right]\left(x-1\right)=0\)

<=> \(\left(x-1\right)^2\left(x^2-5x+1\right)=0\)

<=> \(\orbr{\begin{cases}x=1\\x^2-5x+1=0\left(1\right)\end{cases}}\)

Giải pt (1) ta có: \(\Delta=\left(-5\right)^2-4=21>0\)

=> pt có 2 nghiệm

\(x_1=\frac{5+\sqrt{21}}{2}\); \(x_2=\frac{5-\sqrt{21}}{2}\)

         \(x^2-5x-4\left(x-5\right)=0\)

\(\Leftrightarrow\)\(x\left(x-5\right)-4\left(x-5\right)=0\)

\(\Leftrightarrow\)\(\left(x-5\right)\left(x-4\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x-5=0\\x-4=0\end{cases}}\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x=5\\x=4\end{cases}}\)

Vậy....

\(2x\left(x+6\right)=7x+42\)

\(\Leftrightarrow\)\(2x\left(x+6\right)-7x-42=0\)

\(\Leftrightarrow\)\(2x\left(x+6\right)-7\left(x+6\right)=0\)

\(\Leftrightarrow\)\(\left(x+6\right)\left(2x-7\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x+6=0\\2x-7=0\end{cases}}\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x=-6\\x=\frac{7}{2}\end{cases}}\)

Vậy......

\(x^3-5x^2+x-5=0\)

\(\Leftrightarrow\)\(x^2\left(x-5\right)+\left(x-5\right)=0\)

\(\Leftrightarrow\)\(\left(x-5\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow\)\(x-5=0\)

\(\Leftrightarrow\)\(x=5\)

\(x^4-2x^3+10x^2-20x=0\)

\(\Leftrightarrow\)\(x^3\left(x-2\right)+10x\left(x-2\right)=0\)

\(\Leftrightarrow\)\(x\left(x-2\right)\left(x^2+10\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x-2=0\end{cases}}\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=2\end{cases}}\)

Vậy...

Cứ thay vào rùi thính thui

Mấy bài kia phá tung tóe rồi rút gọn hết sức xong thay x vào, làm câu c thôi nhé:

c) \(C=x^{14}-10x^{13}+10x^{12}-10x^{11}+...+10x^2-10x+10\)

riêng câu này ta thay x = 9 vào luôn, vậy ta có:

\(C=9^{14}-10\cdot9^{13}+10\cdot9^{12}-10\cdot9^{11}+...+10\cdot9^2-10\cdot9+10\)

\(=9^{14}-\left(9+1\right)\cdot9^{13}+\left(9+1\right)\cdot9^{12}-\left(9+1\right)\cdot9^{11}+...+\left(9+1\right)\cdot9^2-\left(9+1\right)\cdot9+10\)

\(=9^{14}-9^{14}-9^{13}+9^{13}+9^{12}-9^{12}-9^{11}+...+9^3+9^2-9^2-9+10\)

\(=-9+10\)

\(=1\)

*\(\left(2x-3\right)^2=\left(x+5\right)^2\)

\(\Rightarrow\left(2x-3\right)^2-\left(x+5\right)^2=0\)

\(\Rightarrow\left(2x-3-x-5\right)\left(2x-3+x+5\right)=0\)

\(\Rightarrow\left(x-8\right)\left(3x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-\dfrac{2}{3}\end{matrix}\right.\)

* \(x^3-16x=0\)

\(\Rightarrow x\left(x^2-16\right)=0\)

\(\Rightarrow x\left(x^2-4^2\right)=0\)

\(\Rightarrow x\left(x-4\right)\left(x+4\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

*\(x^4-2x^3+10x^2-20x=0\)

\(\Rightarrow\left(x^4+10x^2\right)-\left(2x^3+20x\right)=0\)

\(\Rightarrow x^2\left(x^2+10\right)-2x\left(x^2+10\right)=0\)

\(\Rightarrow\left(x^2+10\right)\left(x^2-2x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=\varnothing\\x=2\end{matrix}\right.\)