Xác định giá trị của tham số m để phương trình 2 x 3 + 3m x 2 - 5 = 0 có nghiệm duy nhất.
A. m = 5 3 B. m < 5 3
C. m > 5 3 D. m ∈ R
Xác định giá trị của tham số m để phương trình 2 x 3 + 3m x 2 - 5 = 0 có nghiệm duy nhất.

Đáp án: B.
Với m = 0, phương trình 2 x 3 - 5 = 0 có nghiệm duy nhất.
Với m ≠ 0, đồ thị hàm số y = 2 x 3 + 3m x 2 - 5 chỉ cắt Ox tại một điểm khi y C Đ . y C T > 0. Ta có y' = 6 x 2 + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3 + 3 m 3 - 5 = m 3 - 5.
Suy ra y(0).y(-m) = -5(
m
3
- 5) > 0 ⇔ m < 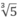
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
1. Tìm tham số m để phương trình 3cos2x-7=2m có nghiệm?
2. Trên đoạn \([0;2\pi]\) , phương trình \(2cos^2x-\sqrt{3}cosx=0\)có bao nhiêu nghiệm?
3. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y=\sqrt{2cosx-3m+14}\) xác định với mọi x thuộc R?
Help me!!!
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
cho hệ phương trình mx-y=2
3x+my=5( m là tham số)
xác định các giá trị của tham số m để hệ phương trình có nghiệm duy nhất(x;y) thỏa mãn x+y=3/m2+3
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}\ne-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
\(\left\{{}\begin{matrix}mx-y=2\\3x+my=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\cdot\left(mx-2\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5+2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x=\dfrac{2m+5}{m^2+3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+5}{m^2+3}\\y=\dfrac{2m^2+5m}{m^2+3}-2=\dfrac{2m^2+5m-2m^2-6}{m^2+3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2m+5}{m^2+3}\\y=\dfrac{5m-6}{m^2+3}\end{matrix}\right.\)
\(x+y=\dfrac{3}{m^2+3}\)
=>\(\dfrac{2m+5+5m-6}{m^2+3}=\dfrac{3}{m^2+3}\)
=>\(7m-1=3\)
=>7m=4
=>m=4/7(nhận)
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
cho phương trình x^2-2(m+2)x+3m+2=0 (m là tham số). tìm tất cả giá trị của m để phương trình có 2 nghiệm x1,x2 thỏa mãn x2-2x1=3
\(\Delta=\left(2m+4\right)^2-4\left(3m+2\right)\)
\(=4m^2+16m+16-12m-8\)
\(=4m^2+4m+8\)
\(=\left(2m+1\right)^2+7>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\x_1x_2=3m+2\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\-2x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2m+1\\x_1+x_2=2m+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2}{3}m+\dfrac{1}{3}\\x_2=2m+4-\dfrac{2}{3}m-\dfrac{1}{3}=\dfrac{4}{3}m+\dfrac{11}{3}\end{matrix}\right.\)
Ta có: \(x_1x_2=3m+2\)
nên \(\left(\dfrac{2}{3}m+\dfrac{1}{3}\right)\left(\dfrac{4}{3}m+\dfrac{11}{3}\right)=3m+2\)
\(\Leftrightarrow m^2\cdot\dfrac{8}{9}+\dfrac{22}{9}m+\dfrac{4}{9}m+\dfrac{11}{9}=3m+2\)
\(\Leftrightarrow m^2\cdot\dfrac{8}{9}-\dfrac{1}{9}m-\dfrac{7}{9}=0\)
\(\Leftrightarrow8m^2-m-7=0\)
\(\Leftrightarrow\left(m-1\right)\left(8m+7\right)=0\)
=>m=1 hoặc m=-7/8
Xác định giá trị của tham số m để hệ phương trình x − ( m − 2 ) y = 2 ( m − 1 ) x − 2 y = m − 5 có nghiệm duy nhất.
A. m ≠ 0
B. m ≠ 2
C. m ≠ {0; 3}
D. m = 0; m = 3
Xét hệ x − ( m − 2 ) y = 2 ( m − 1 ) x − 2 y = m − 5
⇔ ( m − 2 ) y = x − 2 2 y = ( m − 1 ) x − m + 5 ⇔ ( m − 2 ) y = x − 2 y = m − 1 2 x − m 2 + 5 2
TH1: Với m – 2 = 0 ⇔ m = 2 ta có hệ 0. y = x − 2 y = 1 2 x + 3 2 ⇔ x = 2 y = 1 2 x + 3 2
Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng x = 2 và y = 1 2 x + 3 2 cắt nhau
TH2: Với m – 2 ≠ 0 ⇔ m ≠ 2 ta có hệ: ( m − 2 ) y = x − 2 y = m − 1 2 x − m 2 + 5 2 ⇔ y = 1 m − 2 x − 2 m − 2 y = m − 1 2 x − m 2 + 5 2
Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng: d : y = 1 m − 2 x − 2 m − 2 và d ' : y = m − 1 2 x − m 2 + 5 2 cắt nhau
⇔ 1 m − 2 ≠ m − 1 2 ⇔ m – 1 m – 2 ≠ 2 ⇔ m 2 – 3 m + 2 ≠ 2 ⇔ m 2 – 3 m 0
Suy ra m ≠ {0; 2; 3}
Kết hợp cả TH1 và TH2 ta có m ≠ {0; 3}
Vậy hệ phương trình đã cho có nghiệm duy nhất khi m ≠ {0; 3}
Đáp án: C
Cho phương trình $x^2 + 4x + 3m - 2 = 0$, với $m$ là tham số
1. Giải phương trình với $m = -1$.
2. Tìm giá trị của $m$ để phương trình đã cho có một nghiệm $x = 2$.
3. Tìm các giá trị của $m$ để phương trình đã cho có hai nghiệm phân biệt $x_1$, $x_2$ sao cho $x_1 + 2 x_2 = 1$.
a, Thay m = -1 vào phương trình trên ta được
\(x^2+4x-5=0\)
Ta có : \(\Delta=16+20=36\)
\(x_1=\frac{-4-6}{2}=-5;x_2=\frac{-4+6}{2}=1\)
Vậy với m = -1 thì x = -5 ; x = 1
b, Vì x = 2 là nghiệm của phương trình trên nên thay x = 2 vào phương trình trên ta được :
\(4+8+3m-2=0\Leftrightarrow3m=-10\Leftrightarrow m=-\frac{10}{3}\)
Vậy với x = 2 thì m = -10/3
c, Để phương trình có 2 nghiệm phân biệt thì \(\Delta>0\)hay
\(16-4\left(3m-2\right)=16-12m+8=4m+8>0\)
\(\Leftrightarrow8>-4m\Leftrightarrow m>-2\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-4\\x_1x_2=\frac{c}{a}=3m-2\end{cases}}\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow x_1=-4-x_2\)(1)
suy ra : \(-4-x_2+2x_2=1\Leftrightarrow-4+x_2=1\Leftrightarrow x_2=5\)
Thay vào (1) ta được : \(x_1=-4-5=-9\)
Mà \(x_1x_2=3m-2\Rightarrow3m-2=-45\Leftrightarrow3m=-43\Leftrightarrow m=-\frac{43}{3}\)