Cho hình lăng trụ tứ giác đều A B C D . A 1 B 1 C 1 D 1 cạnh đáy bằng 1 và chiều cao bằng x. Tìm x để góc tạo bởi đường thẳng B 1 D và B 1 D 1 C đạt giá trị lớn nhất.
A. 1
B. 0,5
C. 2
D. 2
Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi, A ' AC ^ = 60 o , B ' C = a 3 2 . Tính thể tích lăng trụ ABCA′B′C′.
A. 3 a 3 4
B. 3 3 a 3 4
C. 3 3 a 3 16
D. 3 a 3 16
Đáp án A
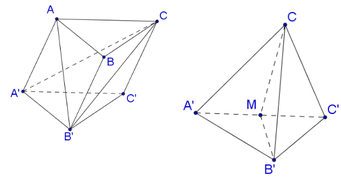
Dễ dàng tính được các cạnh của tứ diện CA′B′C′:
A ' C = A ' C ' = CC ' = B ' C ' = A ' B ' = a .
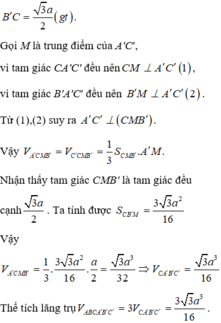
Cho hình lăng trụ tứ giác ABCD. A’B’C’D’. Một mặt phẳng song song với mặt phẳng (A’B’C’D’) cắt các cạnh bên của hình lăng trụ lần lượt tại A”, B”, C”, D”. Hỏi hình tạo bởi các điểm A, B, C, D, A”, B”, C”, D” là hình gì?
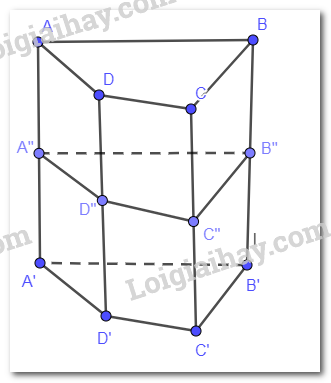
Mặt phẳng (ABCD) song song với (A"B"C"D") (do cùng song song với (A'B'C'D')) nên ABCD.A"B"C"D" là hình lăng trụ tứ giác.
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Cho hình lăng trụ tứ giác đều, cạnh đáy bằng a, cạnh bên bằng b. Diện tích toàn phần của hình lăng trụ là
A. S t p = 2 a 2 + 4 a b .
B. S t p = 2 a 2 + 16 a b .
C. S t p = a 2 + 4 a b .
D. S t p = a 2 + 16 a b .
Đáp án A
S t p = S x q + 2 S d , trong đó S t p là diện tích toàn phần, S d là diện tích đáy, S x q là diện tích xung quanh hình lăng trụ tứ giác đều.
S t p = 4. a . b + 2 a 2 = 2 a 2 + 4 a b .
Cho khối lăng trụ tứ giác đều ABCD. A 'B 'C 'D ' có khoảng cách giữa AB và A’D bằng 2, đường chéo của mặt bên bằng 5. Biết A ' A > A D . Thể tích lăng trụ là
A. V = 30 5
B. V = 10 5 3
C. 10 5
D. 5 5
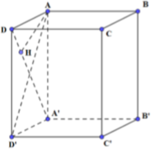
Kẻ
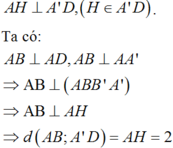
Gọi độ dài đoạn AD là x
∆ A D A ' vuông tại A,
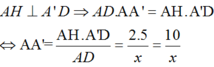
Lại có:
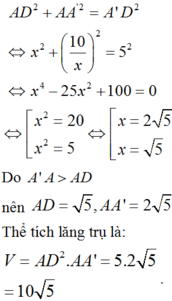
Chọn: C
Một hình lăng trụ đứng ABC.A'B'C'(đáy là tam giác đều ABC) ở bên trong một hình trụ. Các đỉnh A, B, C, A', B', C' thuộc hình trụ. Hình lăng trụ đứng và hình trụ có cùng chiều cao. Cho biết chu vi tam giác ABC là 6cm, thể tích của hình lăng trụ đứng là 123 cm³. Hãy tính chiều cao và thể tích của hình trụ( kết quả làm tròn đến hàng đơn vị)
Chú ý: Thể tích hình trụ đứng = diện tích đáy nhân với chiều cao.
Diện tích tam giác đều là: AB^2√3/4
Thể tích hình trụ = diện tích đáy nhân với chiều cao.
AB=2cm
=>S ABC=căn 3(cm2)
=>h=12(cm)
43:cho hình lăng trụ đứng ABC.EFD có góc ABC=90 độ,CD=6cm,BC=4cm,S tứ giác AEDC=30cm2.
a)Tính AB
b)Tính Stp và V của hình lăng trụ đứng ABC.EFD
44:Hình lăng trụ đứng ABC.A'B'C' có thể tích 56cm3,chiều cao 7cm và đáy là tam giác vuông có 1 cạnh góc vuông là 5cm.Vẽ hình và tính các cạnh còn lại của đáy hình lăng trụ này.
Cho hình lăng trụ tứ giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ đều là
![]()
![]()
![]()
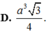
Cho hình lăng trụ tứ giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ đều là
A. 2 a 3 2 3
B. a 3
C. 2 a 3 3
D. a 3 3 4
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. 5 π a 2 3
B. 7 π a 2 3
C. 3 π a 2
D. 11 π a 2 3