Các câu hỏi tương tự
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi
V
1
;
V
2
lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh
V...
Đọc tiếp
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi V 1 ; V 2 lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh V 1 và V 2
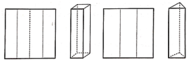
A. V 1 > V 2
B. V 1 = V 2
C. V 1 < V 2
D. Không so sánh được
Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:- Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là
V
1
(Hình 1).- Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là
V
2
(Hình 2).Tính tỉ số
k
V
1
V
2...
Đọc tiếp
Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:
- Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là V 1 (Hình 1).
- Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là V 2 (Hình 2).
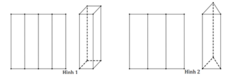
Tính tỉ số k = V 1 V 2
A. k = 3 3 8
B. k = 3 3 2
C. k = 4 3 9
D. k = 3 3 4
Cho hình lăng trụ tam giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ tính theo a bằng A.
a
3
3
B.
2
a
3
2
3
C.
a
3
3
4
D. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ tính theo a bằng
A. a 3 3
B. 2 a 3 2 3
C. a 3 3 4
D. 2 a 3 3
Cho một khối lăng trụ có thể tích là 3 .a 3 , đáy là tam giác đều cạnh a. Tính chiều cao h của khối lăng trụ.
A. h = 4a
B. h = 3a
C. h = 2a
D. 12a
Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a. Khi đó thể tích V của khối lăng trụ trên là A.
V
a
3
3
4
.
B.
V
a
3
4
.
C.
V...
Đọc tiếp
Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a. Khi đó thể tích V của khối lăng trụ trên là
A. V = a 3 3 4 .
B. V = a 3 4 .
C. V = a 3 3 12 .
D. V = a 3 3 12 .
Cho lăng trụ tam giác đều có cạnh đáy bằng 2a và các cạnh bên đều là hình vuông. Tính theo a thể tích khối lăng trụ đã cho. A.
2
a
3
2
3
B.
2
a
3
2
C.
2
a
3...
Đọc tiếp
Cho lăng trụ tam giác đều có cạnh đáy bằng 2a và các cạnh bên đều là hình vuông. Tính theo a thể tích khối lăng trụ đã cho.
A. 2 a 3 2 3
B. 2 a 3 2
C. 2 a 3 2 4
D. 2 a 3 3
Cho khối lăng trụ tam giác đều
A
B
C
.
A
B
C
có cạnh đáy bằng 2, diện tích tam giác ABC bằng 3. Tính thể tích của khối lăng trụ A.
2
5
3
B.
2
C.
2
5
D.
3
2
Đọc tiếp
Cho khối lăng trụ tam giác đều A B C . A ' B ' C ' có cạnh đáy bằng 2, diện tích tam giác A'BC bằng 3. Tính thể tích của khối lăng trụ
A. 2 5 3
B. 2
C. 2 5
D. 3 2
Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể tích khối lăng trụ. A.
2
a
3
3
B.
4
a
3
3
C.
a
3
D.
2
a
3
Đọc tiếp
Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể tích khối lăng trụ.
A. 2 a 3 3
B. 4 a 3 3
C. a 3
D. 2 a 3
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2, diện tích tam giác A’BC bằng 3. Tính thể tích của khối lăng trụ
A. 2 5 3
B. 2
C. 2 5
D. 3 2




