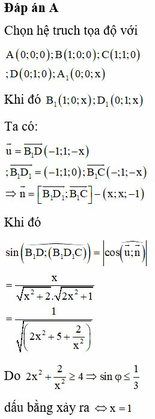Các câu hỏi tương tự
Cho hình lăng trụ tứ giác đều
A
B
C
D
.
A
1
B
1
C
1
D
1
cạnh đáy bằng 1 và chiều cao bằng x. Tìm x để góc tạo bởi đường thẳng
B
1
D
và
B
1
D
1...
Đọc tiếp
Cho hình lăng trụ tứ giác đều A B C D . A 1 B 1 C 1 D 1 cạnh đáy bằng 1 và chiều cao bằng x. Tìm x để góc tạo bởi đường thẳng B 1 D và B 1 D 1 C đạt giá trị lớn nhất.
A. 2
B. x = 1.
C. x = 0,5.
D. x = 2.
Trong không gian Oxyz, cho hai điểm A(1;-2;3),B(-3;0;1) và đường thẳng d:
x
-
2
1
y
+
1
2
z
+
1
-
2
. Điểm M(a;b;c) thuộc d sao cho
M
A
2
+...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;-2;3),B(-3;0;1) và đường thẳng d: x - 2 1 = y + 1 2 = z + 1 - 2 . Điểm M(a;b;c) thuộc d sao cho M A 2 + M B 2 nhỏ nhất. Giá trị biểu thức a+b+c bằng
A. -1.
B. 2.
C. 1.
D. -2.
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x+3y-2z+20 và đường thẳng d:
x
-
1
2
y
+
1
-
1
z
-
4
1
. Đường thẳng qua A(1;2;-1) và cắt (P), d lần lượt tại B và C(a;b;c) sao cho C là...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x+3y-2z+2=0 và đường thẳng d: x - 1 2 = y + 1 - 1 = z - 4 1 . Đường thẳng qua A(1;2;-1) và cắt (P), d lần lượt tại B và C(a;b;c) sao cho C là trung điểm của AB. Giá trị của biểu thức a+b+c bằng
A. -5
B. -12
C. -15
D. 11
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
Δ
:
x
+
1
2
y
3
z
+
1
−
1
và hai điểm
A
1
;
2
;
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x + 1 2 = y 3 = z + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi M a ; b ; c là giao điểm của d với đường thẳng Δ . Giá trị P = a + b + c bằng
A. -2
B. 4
C. 2
D. 6
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng
30
°
. Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng A.
a
15
15
B.
a
15
5
C.
a
3
13...
Đọc tiếp
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng 30 ° . Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng
A. a 15 15
B. a 15 5
C. a 3 13
D. a 39 13
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng
30
°
. Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng A. a
15
15
B. a
15
5
C. a
3
13
D. a
39
13
Đọc tiếp
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng 30 ° . Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng
A. a 15 15
B. a 15 5
C. a 3 13
D. a 39 13
Cho hàm số
y
−
x
+
1
2
x
−
1
có đồ thị là (C), đường thẳng
d
:
y
x
+
m
. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi
k
1
,
k
2...
Đọc tiếp
Cho hàm số y = − x + 1 2 x − 1 có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. m = -1
B. m = -2
C. m = 3
D. m = -5
Cho lăng trụ tam giác ABC.A′B′C′ có độ dài cạnh bên bằng 4 và khoảng cách từ điểm A đến các đường thẳng BB′,CC′ lần lượt bằng 1 và 2. Biết góc giữa hai mặt phẳng (ABB′A′) và (ACC′A′) bằng
60
°
. Tính thể tích khối lăng trụ ABC.A′B′C′. A. 4
3
B.
3
C. 3
3
D. 2
3
Đọc tiếp
Cho lăng trụ tam giác ABC.A′B′C′ có độ dài cạnh bên bằng 4 và khoảng cách từ điểm A đến các đường thẳng BB′,CC′ lần lượt bằng 1 và 2. Biết góc giữa hai mặt phẳng (ABB′A′) và (ACC′A′) bằng 60 ° . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 4 3
B. 3
C. 3 3
D. 2 3
Trong không gian Oxyz, có hai mặt phẳng (P),(Q) cách đều hai điểm A(3;-2;0),B(1;0;2) và chứa đường thẳng d:
x
-
1
3
y
-
1
1
z
+
1
-
2...
Đọc tiếp
Trong không gian Oxyz, có hai mặt phẳng (P),(Q) cách đều hai điểm A(3;-2;0),B(1;0;2) và chứa đường thẳng d: x - 1 3 = y - 1 1 = z + 1 - 2 . Giá trị sin góc tạo bởi hai mặt phẳng (P) và (Q) bằng
A. 2 3
B. 3 2
C. 7 3
D. 1 3