Cho \(\Delta ABC\), gọi trung điểm của BC là M.
CMR: \(AM<\frac{AB+AC}{2}\)
Những câu hỏi liên quan
9 tháng 1 2022 lúc 20:21
Cho \(\Delta\)\(ABC\) cân tại \(A\). Gọi \(M\) là trung điểm của cạnh \(BC\). Chứng minh:
a) \(AM\) \(\bot\) \(BC\)
b) \(AM\) là tia phân giác của góc \(BAC\)
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác của góc BAC
Đúng 1
Bình luận (0)
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác của góc BAC
Đúng 2
Bình luận (2)
Câu trả lời:
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác của góc BAC
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc cân tại a (ab = ac), m là trung điểm bc. gọi d là điểm nằm giữa a và m.CMR:
a) am là tia phân giác của góc a
b) tam giác abc = tam giác acd
c) tam giác bcd là tam giác cân
cho \(\Delta\)ABC vuông tại A, đường cao AH.
a, CM: \(\Delta\)AHC đồng dạng \(\Delta\)BHA.
b, Cho AB = 15 cm, AC = 20 cm. Tính BC, AH.
c, Gọi M là trung điểm của BH, N là trung điểm AH. CMR: CN\(\perp\)AM.
Cho \(\Delta ABC=\Delta A'B'C'\) .Kẻ \(AH\perp BC\)tại H'.
a, C/minh: AH = A'H'
b, Gọi M là trung điểm của BC, M' là trung điểm của B'C'. C/minh: AM = A'M'
Bài 4: Cho tam giác ABC; gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao MD MA. a) Chứng minh: Delta ABMDelta DCM b) Chứng minh: AB // CD c) Kẻ BHperp AMleft(Hvarepsilon AMright), CKperp DMleft(Kvarepsilon DMright), cho biết MK 1,5cm. Tính độ dài của đoạn thẳng HK.Bài 5:Cho 3 số thực a, b, c thỏa mãn dfrac{a}{2015}dfrac{b}{2016}dfrac{c}{2017}Chứng minh rằng: 4(a – b)(b – c) (c – a)2.
Đọc tiếp
Bài 4:
Cho tam giác ABC; gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao MD = MA.
a) Chứng minh: \(\Delta ABM=\Delta DCM\)
b) Chứng minh: AB // CD
c) Kẻ \(BH\perp AM\left(H\varepsilon AM\right),\) \(CK\perp DM\left(K\varepsilon DM\right)\), cho biết MK = 1,5cm. Tính độ dài của đoạn thẳng HK.
Bài 5:
Cho 3 số thực a, b, c thỏa mãn \(\dfrac{a}{2015}=\dfrac{b}{2016}=\dfrac{c}{2017}\)
Chứng minh rằng: 4(a – b)(b – c) = (c – a)2.
4:
b: Xét tứ gác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//CD
Đúng 1
Bình luận (0)
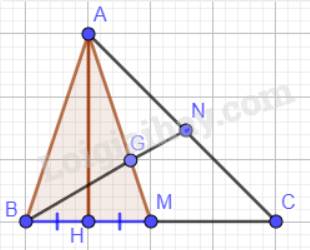
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).
Đúng 0
Bình luận (0)
Bài 17: Cho tam giác ABC cân tại A. Gọi M là trung điểm BC.
a, Chứng minh \(\Delta\) ABM =\(\Delta\) ACM
b, Chứng minh AM là phân giác góc BAC và AM vuông góc BC.
c, Lấy E bất kì trên đoạn AM. Chứng minh tam giác EBC cân.
Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
Đúng 2
Bình luận (0)
Trên ba cạnh AB; AC: BC của tam giác đều ABC . Lấy các điểm theo thứ tự M; N; P sao cho AM = BN = CP. Gọi O là giao điểm 3 đường trung trực của \(\Delta ABC\). C/minh O cũng là giao điểm ba đường trung trực của \(\Delta MNP\).
24 tháng 2 2023 lúc 23:05
Cho \(\Delta ABC\), đường trung tuyến AM. Tia phân giác \(\widehat{AMB}\) cắt AB tại D, tia phân giác \(\widehat{AMC}\) cắt AC tại E. Gọi I là giao điểm của AM và DE. Hỏi \(\Delta ABC\) cần có điều kiện gì để DE là đường trung bình của \(\Delta ABC\)?
AD/DB=AM/MB
AE/EC=AM/MC
mà MB=MC
nên AD/DB=AE/EC
=>DE//BC
Để DE là đừog trung bình của ΔABC thì AD/DB=AE/EC=1
=>AM/MB=AM/MC=1
=>ΔABC vuông tại A
Đúng 2
Bình luận (0)
Cho \(\Delta\)ABC có AB < AC. Gọi M là trung điểm của cạnh BC, (đoạn thẳng AM được gọi là đường trung tuyến của \(\Delta\)ABC). Lấy điểm I bất kì trên đường trung tuyến AM. Trên tia đối của tia MA lấy E sao cho ME = MI. So sánh \(\Delta\)BMI và \(\Delta\)MEC.
Xét ΔBMI và ΔCME có
MI=ME
góc BMI=góc CME
MB=MC
Do đó: ΔBMI=ΔCME
Đúng 0
Bình luận (0)