Có tất cả bao nhiêu cặp số thực (x,y) sao cho x ∈ - 1 ; 1 và ln ( x - y ) x - 2017 y + e 2018 . Biết rằng giá trị lớn nhất của biểu thức P = e 2018 ( y + 1 ) x 2 - 2018 x 2 với ( x ; y ) ∈ S đạt được tại (x0, y0). Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho x là số nguyên dương và y là số thực. Có tất cả bao nhiêu cặp số \(\left(x;y\right)\) thỏa mãn \(ln\left(1+x+2y\right)=2y+3x-10\) ?
Câu 8:
Có tất cả bao nhiêu cặp số tự nhiên :x,y sao cho (2x+1)(2y-3)=10
Do 10 = 1.10 =10.1 = 2.5 = 5.2
Mà 2x + 1 lẻ nên 2x + 1 = 1 hoặc 2x + 1 = 5
=> x = 0 hoặc 2 nhưng x = 0 thì x.y = 0 nên ta chọn x = 2 khi đó y - 3 = 2
=> y = 5
Vậy khi đó x.y lớn nhất là : x.y = 2.5 = 10
Có tất cả bao nhiêu cặp số thực (x;y) sao cho x ∈ [ - 1 ; 1 ] và ln x - y x - 2017 y + e 2018 . Biết rằng giá trị lớn nhất của biểu thức P = e 2018 y + 1 x 2 - 2018 x 2 với x ; y ∈ S đạt được tại x 0 ; y 0 . Mệnh đề nào sau đây đúng?
A. x 0 ∈ - 1 ; 0
B. x 0 = - 1
C. x 0 = 1
D. x 0 ∈ [ 0 ; 1 )
Đáp án A
Ta có ln x - y 2 - 2017 x = ln x - y y - 2017 y + e 2018 ⇔ x - y ln x - y - 2017 x - y = e 2018
⇔ ln x - y - e 2018 x - y - 2017 = 0 . Xét hàm số f t = ln t - e 2018 t - 2017 ,có f ' t = 1 t + e 2018 t 2 > 0 ; ∀ t > 0
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f e 2018 = 0 ⇒ t = x - y = e 2018
Khi đó P = e 2018 x 1 + x - e 2018 - 2018 x 2 → g x
Lại có g ' x = e 2018 x x 2019 + 2018 x - 2018 e 2018 - 4036 x ⇒ g ' ' < 0 ; ∀ x ∈ - 1 ; 1
Nên g'(x) là hàm số nghịch biến trên [-1;1] mà g ' - 1 = e - 2018 + 2018 > 0
Và g ' 0 = 2019 - 2018 e 2018 < 0 nên tồn tại x 0 ∈ - 1 ; 0 sao cho g ' x 0 = 0
Vậy m a x - 1 ; 1 g x = g x 0 hay giá trị lớn nhất của P đạt được khi x 0 ∈ - 1 ; 0 .
Có tất cả bao nhiêu cặp số thực (x; y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - ( y + 4 ) và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Chọn B.
Với ![]() ,
,
xét từng TH phá dấu trị tuyệt đối, ta tìm được nghiệm
-3 ≤ y ≤ 0
Khi đó 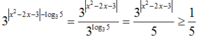 và
và ![]()
Do đó
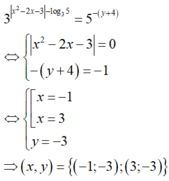
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8 , xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0 .
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5 và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5 .
Do đó 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 ⇔ [ x = - 1 x = 3 y = - 3 ⇒ x ; y = - 1 ; - 3 ; 3 ; - 3 .
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - ( y + 4 ) và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện 3 x 2 − 2 x − 3 − log 3 5 = 5 − y + 4 và 4 y − y − 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3.
B. 2.
C. 1.
D. 4.
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8
xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5
và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5
Do đó
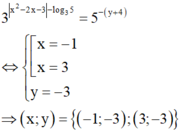
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
Có tất cả bao nhiêu cặp số nguyên (x, y) thỏa mãn: |x| + |y| = 1
\(\left|x\right|+\left|y\right|=1=0+1\)
TH1: \(\left\{{}\begin{matrix}\left|x\right|=0\\\left|y\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\pm1\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}\left|x\right|=1\\\left|y\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\pm1\\y=0\end{matrix}\right.\)
Ta có: |x|+|y|=1
nên \(\left(\left|x\right|,\left|y\right|\right)\in\left\{\left(0;1\right);\left(1;0\right)\right\}\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(0;-1\right);\left(0;1\right);\left(-1;0\right);\left(1;0\right)\right\}\)