Chọn C.

Ta có : 

Ta đi xét các phương án:

Phương án  A:  nên  

Loại A.

Phương án B:  

Loại B.

Phương án C:  

Chọn C.

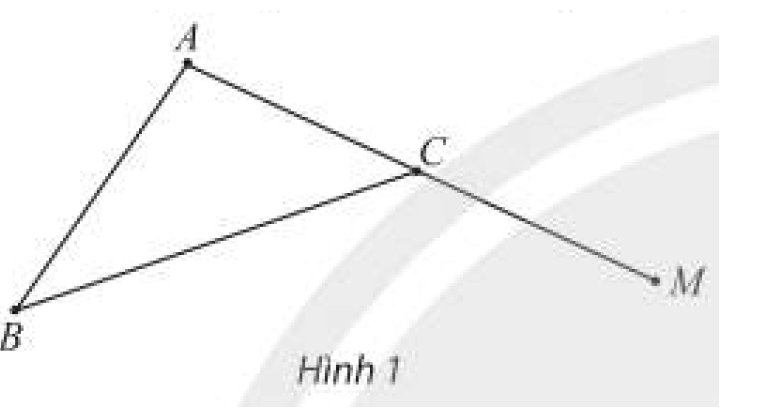
\(\left. \begin{array}{l}M \in AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow M \in \left( {ABC} \right)\). Vậy mệnh đề A đúng.

\(\left. \begin{array}{l}C \in AM\\AM \subset \left( {ABM} \right)\end{array} \right\} \Rightarrow C \in \left( {ABM} \right)\). Vậy mệnh đề B đúng.

\(\left. \begin{array}{l}A \in CM\\CM \subset \left( {MBC} \right)\end{array} \right\} \Rightarrow A \in \left( {MBC} \right)\). Vậy mệnh đề C đúng.

Vậy mệnh đề D sai.

Chọn D.

Chọn C.

Độ dài các cạnh của tam giác là a thì độ dài các vectơ

Độ dài các cạnh của tam giác là a thì độ dài các vectơ

Chọn C

P: “tam giác ABC vuông tại A”

Q: “tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”

+) Mệnh đề \(Q \Rightarrow P\) là “Nếu tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)thì tam giác ABC vuông tại A”

+) Từ định lí Pytago, ta có:

Tam giác ABC vuông tại A thì \(A{B^2} + A{C^2} = B{C^2}\)

Và: Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) thì vuông tại A.

Do vậy, hai mệnh đề “\(P \Rightarrow Q\)” và “\(Q \Rightarrow P\)” đều đúng.

a: Nếu AB=BC=CA thì ΔBAC không là tam giác đều

Do a, b, c là độ dài ba cạnh của một tam giác nên theo bất đẳng thức tam giác ta có:

*  a < b + c ⇔ a 2 < a b + c ⇔ a 2 < a b + a c

*  a + c > b ⇔ b a + c > b 2 ⇔ a b + b c > b 2

*  b - c < a ⇔ b - c 2 < a 2 ⇔ b 2 - 2 b c + c 2 < a 2 ⇔ b 2 + c 2 < a 2 + 2 b c

Do đó, mệnh đề D không đúng.

A. “Tam giác đều là tam giác có ba cạnh bằng nhau.” Là một mệnh đề đúng

B. “\(3\;\, < 1\)” là một mệnh đề sai

C. “\(4 - 5 = 1\)” là một mệnh đề sai

D. “Bạn học giỏi quá!” là câu cảm thán, không xác định được tính đúng sai nên không là một mệnh đề.

Chọn D.