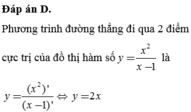Viết phương trình đường thẳng biết đồ thị của nó đi qua A(2;-5)và // đường thẳng (d):2x-1

Những câu hỏi liên quan
cho hàm số y=ax2
a) xác định hệ số a biết đồ thị (P) của nó đi qua A(4;4)
b) viết phương trình đường thẳng (d) đi qua A và tiếp xúc với (P)
a) đồ thi của hàm số đi qua A ( 4;4 ) nên x = y = 4
Thay vào hàm số y = ax2,ta có :
4 = 42 . a\(\Rightarrow\)a = 0,25
b) gọi đường thẳng ( d ) là : y = bx + c
vì ( d ) đi qua A nên 4 = 4b + c
Xét phương trình hoành độ giao điểm, ta có : 0,25x2 = bx + c
\(\Rightarrow x^2=\frac{bx+c}{0,25}=4bx+4c\)
\(\Leftrightarrow x^2-4bx-4c=0\)
\(\Leftrightarrow x^2-4bx-4\left(4-4b\right)=0\)
\(\Leftrightarrow x^2-4bx+16b-16=0\)
( d ) tiếp xúc với ( P ) nên : \(\Delta=\left(4b\right)^2-4\left(16b-16\right)=0\)
\(=16b^2-64b+64=\left(4b-8\right)^2=0\)
\(\Leftrightarrow b=2\)
suy ra c= -4
vậy pt đường thẳng ( d ) là y = 2x - 4
a)Viết phương trình đường thẳng \(\left(\Delta\right)\)biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và cắt trục hoành tại điểm có hoành độ bằng -3
b) Viết phương trình đường thẳng (d) biết (d) có hệ số góc là -2 và đi qua (-1;5)
GIÚP TỚ VỚI :<< TỚ ĐANG CẦN GẤP Ạ
cho hàm số : y= (m-2)x+3 (d)
a, tìm m=? biết đồ thị (d) đi qua A (1, -1) . vẽ đồ thị hàm số với m vừa tìm đc
b, viết phương trình đường thẳng đi qua điểm B (-2 ,2) và song song với đường thẳng vừa tìm đc ở câu a
â ) vì đồ thị ( đ ) đi qua A ( 1 ; -1 ) nên thay x = 1 ; y = -1 vào đồ thị ( d )
ta có : - 1 = ( m - 2 ) . 1 + 3
<=> ( m - 2 ) + 3 = -1
<=> m - 2 = - 4
<=> m = -2
Vậy m = 1
| x | 0 | \(\frac{3}{4}\) |
| y=(-2 - 2 ) x + 3 | 3 | 0 |
b )
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = (m+1)x – 2 có đồ thị là (d)
a. Tìm m biết rằng đồ thị (d) của hàm số đi qua A(-2:0)
b. Nêu tính chất và vẽ đồ thị hàm số với m tìm được ở câu a .
c. Không tính hãy so sánh f(2√3) và f(3√2)
d. Viết phương trình đường thẳng đi qua B(-1;1)và vuông góc với (d) nói trên
Cho hàm số \(y=\frac{1}{2}x-1\) Viết phương trính đường thẳng y=ax+b (\(a\ne0\)) biết đồ thị của nó song song với đường thẳng D và đi qua điểm M (-2;3)
Lời giải:
Vì đường thẳng \((y=ax+b)\parallel (y=\frac{1}{2}x-1)\Rightarrow a=\frac{1}{2}\)
Mà \(M(-2;3)\in (y=ax+b)\) nên \(3=\frac{1}{2}(-2)+b\Rightarrow b=4\)
Do đó PTĐT là \(y=\frac{1}{2}x+4\)
Đúng 0
Bình luận (0)
Vẽ đồ thị (P) của hàm số y=\(-2x^2\) trên mặt phẳng tọa độ Oxy
1. Gọi (d) là đường thẳng đi qua điểm A (-2;-1) và có hệ số góc k
a. Viết phương trình đường thẳng (d)
b. Tìm k để (d) đi qua B nằm trên (P) biết hoành độ của B là 1.
a)Gọi pt đường thẳng d là: \(y=ax+b\left(a\ne0\right)\)
Vì d có hệ số góc là k \(\Rightarrow a=k\)
Vì (d) đi qua điểm \(A\left(-2;-1\right)\Rightarrow-1=-2k+b\Rightarrow b=\dfrac{1}{2k}\)
\(\Rightarrow\left(d\right):y=kx+\dfrac{1}{2k}\)
b) Vì điểm \(B\in\left(P\right)\Rightarrow y_B=-2x_B^2=-2\Rightarrow B\left(1;-2\right)\)
\(\Rightarrow-2=k+\dfrac{1}{2k}\Leftrightarrow-2=\dfrac{2k^2+1}{2k}\Rightarrow-4k=2k^2+1\)
\(\Rightarrow2k^2+4k+1=0\)
\(\Delta=4^2-4.2=8\)
\(\Rightarrow\left[{}\begin{matrix}k=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-4-\sqrt{8}}{4}=\dfrac{-2-\sqrt{2}}{2}\\k=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-4+\sqrt{8}}{4}=\dfrac{-2+\sqrt{2}}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).
Điểm cực đại A(-2; 5) và điểm cực tiểu B(0; 1).
⇒ vtcp của đường thẳng AB: 
⇒ vtpt của AB: 
Đường thẳng AB : qua A( -2 ; 5) và có VTPT  nên có phương trình:
nên có phương trình:
2(x+2)+ 1( y – 5) = 0 hay 2x + y - 1 = 0
Đúng 0
Bình luận (0)
Cho hàm số y=-2x-2 có đồ thị là đường thẳng d1 A/ viết phương trình đường thẳng d2 biết rằng d2 đi qua điểm M (2;-2) và song song với đường thẳng d1 B/ vẽ d1 và d2 trên cùng một hệ trục tọa độ Oxy C/ cho hàm số y= x+m có đồ thị là đường thẳng d3, xác định tham số m để đường thẳng d1 cắt đường thẳng d3 trên trục Ox
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
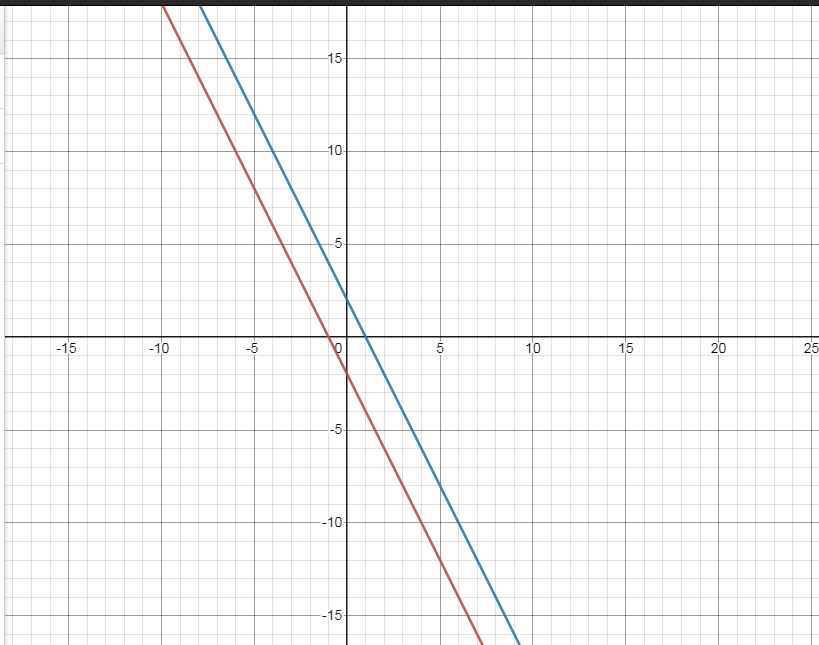
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)
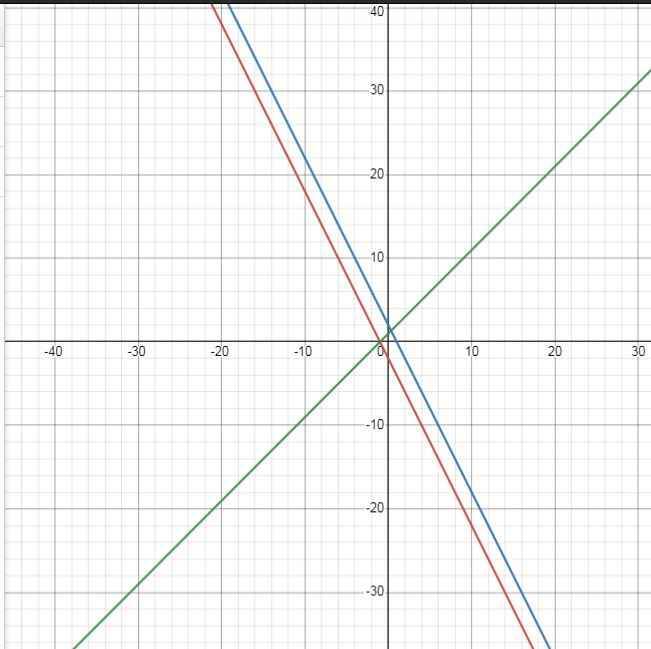
Đúng 1
Bình luận (0)
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
y
x
2
x
−
1
A.
y
4
x
+
1.
B.
y
2
x
+
3.
C.
y
2
x
−
1.
D.
y...
Đọc tiếp
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x 2 x − 1
A. y = 4 x + 1.
B. y = 2 x + 3.
C. y = 2 x − 1.
D. y = 2 x .
Đáp án D.
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x 2 x − 1 là y = ( x 2 ) ' ( x − 1 ) ' ⇔ y = 2 x
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
y
x
2
x
−
1
A.
y
4
x
+
1.
B.
y
2
x
+
3
.
C.
y
2
x
-
1
.
D.
y...
Đọc tiếp
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x 2 x − 1
A. y = 4 x + 1.
B. y = 2 x + 3 .
C. y = 2 x - 1 .
D. y = 2 x .