Tìm tọa độ điểm M' đối xứng với M - 1 ; - 2 ; 3 qua trục Ox.
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy cho điểm M(xo, yo).
a) Tìm tọa độ của điểm A đối xứng với M qua trục Ox;
b) Tìm tọa độ của điểm B đối xứng với M qua trục Oy;
c) Tìm tọa độ của điểm C đối xứng với M gốc O.
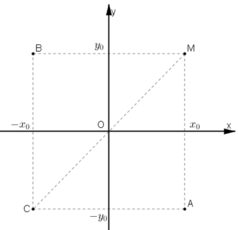
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(x_0;y_0\right)\) :
a) Tìm tọa độ của điểm A đối xứng với M qua trục Ox
b) Tìm tọa độ của điểm B đối xứng với M qua trục Oy
c) Tìm tọa độ điểm C đối xứng với M qua gốc O
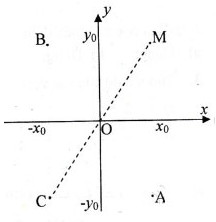
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)
Trong các mặt phẳng Oxy cho điểm (x0; y0)
a) Tìm tọa độ điểm A đối xứng với M qua trục Ox;
b) Tìm tọa độ điểm B đối xứng với M qua trục Oy;
c) Tìm tọa độ điểm C đối xứng với M qua gốc O.
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M’ đối xứng với M qua d.
A. M'(3;-3;0)
B. M'(1;-3;2)
C. M'(0;-3;3)
D. M'(-1;-2;0)
Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M(2 ; 1) qua phép đối xứng tâm I(3 ;-2).
A. M'(1;-3)
B. M'(-5;4)
C. M'(4;-5)
D. M'(1;5)
Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M(2 ; 1) qua phép đối xứng tâm I(3 ;-2).
A. M’(1 ;-3)
B. M’ (-5 ; 4)
C. M’(4 ;-5)
D. M’(1 ;5)
Đáp án C
Phương pháp: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Cách giải: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Ta có
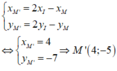
Trong hệ tọa độ Oxy Tìm tọa độ điểm M' đối xứng với điểm M(2;-3) qua trục Oy .
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; − 3 ; 1 và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M' đối xứng với M qua d.
A. M ' 3 ; − 3 ; 0 .
B. M ' 1 ; − 3 ; 2 .
C. M ' 0 ; − 3 ; 3 .
D. M ' − 1 ; − 2 ; 0 .
Đáp án C
d : x = − 1 + 2 t y = − 2 − t , t ∈ ℝ z = 2 t .
Gọi H là hình chiếu của M trên d ⇒ H − 1 + 2 t ; − 2 − t ; 2 t .
⇒ M H → = − 3 + 2 t ; 1 − t ; − 1 + 2 t
Ta có − 3 + 2 t .2 + 1 − t . − 1 + − 1 + 2 t .2 = 0 ⇔ t = 1 ⇒ H 1 ; − 3 ; 2
Suy ra M ' 0 ; − 3 ; 3 .
Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(4;3\right)\). Tìm tọa độ của các điểm A, B, C trong các trường hợp sau :
a) A đối xứng với M qua trục Ox
b) A đối xứng với M qua trục Oy
c) C đối xứng với M qua gốc O
a) Hai điểm đối xứng nhau qua trục Ox sẽ có cùng hoành độ và tung độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(4;-3\right)\).
b) Hai điểm đối xứng qua trục Oy sẽ có cùng tung độ và hoành độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(-4;3\right)\).
c) \(A\left(x,y\right)\) có điểm A' đối xứng qua gốc O thì \(A'\left(x';y'\right)\).
\(M\left(4;3\right)\Rightarrow C\left(-4;-3\right)\).