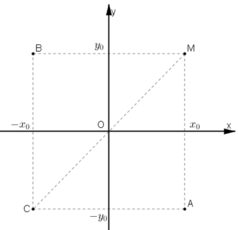
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
Trong hệ tọa độ Oxy Tìm tọa độ điểm M' đối xứng với điểm M(2;-3) qua trục Oy .
Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
Trong mặt phẳng tọa độ Oxy , cho A(2; 1) . Điểm B là điểm đối xứng của A qua trục hoành. Tọa độ điểm B là:
trong mặt phẳng tọa độ oxy cho 2 điểm a(1;4) b(-5;6) tìm tọa độ b' đối xứng với b qua a
Trong mp(Oxy) cho A(-3;2); B(6;1), C(0;4).
a) Chứng tỏ A, B, C là 3 điểm không thẳng hàng.
b) Tìm tọa độ điểm D sao cho ABDC là hình bình hành.
c) Tìm tọa độ điểm E sao cho B là trọng tâm của OAE.
d) Gọi A’ là điểm đối xứng của A qua trục Ox. Tìm giao
điểm của đường thẳng A’B với trục Ox.
e) Tìm điểm M trên Ox sao cho AM + MB ngắn nhất.
Trong mp(Oxy) cho A(-3;2); B(6;1), C(0;4).
a) Chứng tỏ A, B, C là 3 điểm không thẳng hàng.
b) Tìm tọa độ điểm D sao cho ABDC là hình bình hành.
c) Tìm tọa độ điểm E sao cho B là trọng tâm của OAE.
d) Gọi A’ là điểm đối xứng của A qua trục Ox. Tìm giao điểm của đường thẳng A’B với trục Ox.
e) Tìm điểm M trên Ox sao cho AM + MB ngắn nhất
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm M’ đối xứng với điểm M qua điểm P là:
A. M’(18; 10)
B. M’(18; –10)
C. M'(9/2; 1/2)
D. M’(9; – 7)
Trong mặt phẳng tọa độ Oxy, cho các điểm M(0,4) và P(9, -3) .Tọa độ điểm N đối xứng với điểm M qua điểm P là : A. N(18,10) B. N(18, -10) C. N(9/2 ; 1/2) D. N(9; -7)
Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
