bán kính AB có sai không

gọi I là giao điểm của SO với đường tròn.

theo tính chất hai tiếp tuyến cắt nhau ,ta có:

\(\widehat{AOS}=\widehat{SOD}\)\(=sđ\widebat{AI}=sđ\widebat{ID}\)

mà  \(\widehat{ABD}=\frac{sđ\widebat{AD}}{2}=sđ\widebat{AI}\)

\(\Rightarrow\widehat{AOS}=\widehat{ABD}\)(đồng vị)

\(\Rightarrow SO//BD\)

Đg kính AB

Gợi ý:

a) \(DO\) song song với \(EC\) do chúng cùng vuông góc với \(BE\).

b) \(\Delta AEO\sim\Delta ABD\left(g.g\right)\Rightarrow\dfrac{AE}{AB}=\dfrac{AO}{AD}\Rightarrow AO.AB=AE.AD\).

c) \(B,O,E,N\) cùng thuộc đường tròn đường kính \(BN\) do \(\widehat{BON}=\widehat{BEN}=90^o\). 

Mà \(B,O,E,D\) cùng thuộc đường tròn đường kính \(OD\) do \(\widehat{DBO}=\widehat{OED}=90^o\)

nên \(B,O,E,N,D\) cùng thuộc một đường tròn

và \(BN,OD\) cắt nhau tại trung điểm mỗi đường. 

Suy ra tứ giác \(BOND\) là hình bình hành. 

Từ đó suy ra tứ giác \(ODNC\) là hình bình hành. 

Giúp mình giải 3 với 4 với mn

Gọi N là giao điểm của AD và BC; H là giao điểm của MN và AB

Chứng minh góc AHM= 90; mà góc CAB 45(gt) nên tam giác AHM vuông cân

=>MH = AH

=>MH + HB = AH + HB = 2R (1)

* Tam giác MHB vuông tại H

 HB = MB.cos MBH => MB= \(\frac{HB}{sosMBH}\)=\(\frac{HB}{cos60^0}\)=2HB

MH = MB. sin MBH => MH= MB. sin60=\(\frac{MB\sqrt{3}}{2}=HB\sqrt{3}\)

=> \(HB=\frac{MH}{\sqrt{3}}=\frac{\sqrt{3}MH}{3}\)  (2)

Từ (1) và (2) ta có \(MH+\frac{\sqrt{3}MH}{3}=2R\Rightarrow MH=\frac{6R}{3+\sqrt{3}}=\left(3-\sqrt{3}\right)R\)

Vậy \(S=\frac{AB.MH}{2}=\frac{1}{2}.2R\left(3-\sqrt{3}\right)R=\left(3-\sqrt{3}\right)R^2\)

cảm ơn bạn, mình còn rất nhiều bt vì mình đang ôn đội tuyển, mong đc các bạn giúp đỡ

làm sao để Cm góc AHM = 90 độ v ??

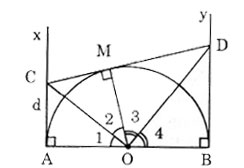a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.

Theo tính chất của hai tiếp tuyến cắt nhau ta có:

CM = CA; DM = DB;

∠O1 = ∠O2; ∠O3 = ∠O4

⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).

⇒ ∠OCD = 900

b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA

Tương tự:

DM = DB

⇒ CM + DM = CA + DB

⇒ CD = AC + BD.

c) Ta có OM ⊥ CD

Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển

OM2 = CM.DM

Mà OM = OA = OA = AB/2 và CM = AC; DM = BD

Suy ra AC.BD = AB2/2 = không đổi

a: Xét (O) có

DC,DA là tiếp tuyến

=>DC=DA và OD là phân giác của góc COA

=>OD vuông góc AC

Xét (O) có

EC,EB là tiếp tuyến

=>EB=EC và OE là phân giác của góc COB(2)

=>OE là trung trực của BC

=>OE vuông góc CB

AD+BE=DC+CE=DE

b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ

Xét tứ giác CMON có

góc CMO=góc CNO=góc MON=90 độ

=>CMON là hình chữ nhật

c: OM*OD+ON*OE

=OC^2+OC^2

=2*R^2ko đổi