Đạo hàm của hàm số ![]() là:
là:
A.  .
.
B. 
C. .
.
D.  .
.
Đạo hàm của hàm số y = x(lnx - 1) là:
A. lnx - 1 B. lnx
C. (1/x) - 1 D. 1
Đạo hàm của hàm số y = x(lnx - 1) là:
A. lnx - 1 B. lnx
C. (1/x) - 1 D. 1
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
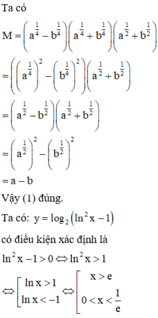
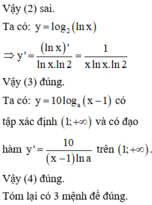
Xét các số thực c > b > a > 0 . Cho hàm số y = f x có đạo hàm liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 . Số điểm cực trị của hàm số y = g x là
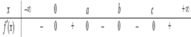
![]()
![]()
![]()
![]()
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng
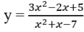
C. Hàm số 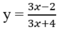 luôn nghịch biến;
luôn nghịch biến;
D. Hàm số
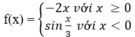
không có đạo hàm tại x = 0.
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 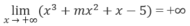
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Cho các mệnh đề sau:
1. Nếu hàm số y = f x liên tục, có đạo hàm tới cấp hai trên a ; b , x 0 ∈ a ; b và f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x0 là một điểm cực trị của hàm số.
2. Nếu hàm số y = f x xác định trên a ; b thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
3. Nếu hàm số y = f x liên tục trên a ; b thì hàm số có đạo hàm tại mọi x thuộc [a;b].
4. Nếu hàm số y = f x có đạo hàm trên a ; b thì hàm số có nguyên hàm trên a ; b
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Đáp án A.

Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]
Chứng minh khẳng định trong nhận xét trên.
a) Đạo hàm của hàm hằng bằng 0: c ’ = 0 .
b) Đạo hàm của hàm số y = x bằng 1: x ’ = 1 .
a) Hàm hằng ⇒ Δy = 0
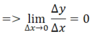
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
a) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
Cho hàm số: y = x 2 - 2 x x + 1 C
a) Đạo hàm của hàm số đã cho tại x=1 là:
A. 1/4
B. (-1)/2
C. 0
D. 1/2
a) với ∆x là số gia của đối số tại x=1, ta có
Δ y = ( 1 + Δ x ) 2 − 2 ( 1 + Δ x ) 1 + Δ x + 1 − 1 − 2 1 + 1 = 1 + 2 Δ x + ( Δ x ) 2 − 2 − 2 Δ x 2 + Δ x + 1 2 = ( Δ x ) 2 − 1 2 + Δ x + 1 2 = 2 ( Δ x ) 2 − 2 + 2 + Δ x 2 ( 2 + Δ x ) = 2 ( Δ x ) 2 + Δ x 2 ( 2 + Δ x ) = ( 2 Δ x + 1 ) . Δ x 2 ( 2 + Δ x ) Δ y Δ x = 2 Δ x + 1 2 ( 2 + Δ x )
Vậy y’(1) =1/4.
Đáp án A
Đạo hàm của hàm số \(y=\left(ax+b\right)sinx+\left(cx+d\right)cosx\). tinh \(a+b+2c+d\)?
Hở, là sao nhỉ? Đạo hàm xong nhưng tính a+b+2c+d kiểu gì?