Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 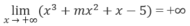
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 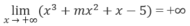
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7
C. Hàm số y = 3 x - 2 3 x + 4 luôn nghịch biến;
D. Hàm số f x = - 2 x với x ≥ 0 sin x 3 với x < 0
không có đạo hàm tại x = 0.
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số 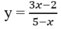 là y = -3;
là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
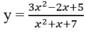
Cho hàm số y = x 2 có các khẳng định sau
I. Tập xác định của hàm số là D= ( 0; + ∞) .
II. Hàm số luôn đồng biến với mọi x thuộc tập xác định của nó.
III. Hàm số luôn đi qua điểm M( 1;1) .
IV. Đồ thị hàm số không có tiệm cận.
Hỏi có bao nhiêu khẳng định đúng?
A. 2
B. 3
C. 4
D. 1
Cho hàm số y = f x xác định trên D = ℝ \ - 2 ; 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên sau
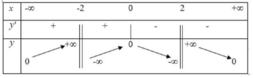 Có bao nhiêu khẳng định đúng trong các khẳng định sau?
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I). Đồ thị hàm số có 2 tiệm cận.
(II). Hàm số đạt giá trị lớn nhất bằng 0.
(III). Hàm số có đúng 1 điểm cực trị.
(IV). Đồ thị hàm số có 3 tiệm cận.
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D=R\{3}.
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị.
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. 1,2,3.
B. 3,4.
C. 2,3,4.
D. 1,4.
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=f(x). Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
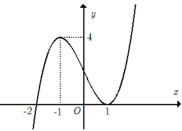
A. Hàm f(x) nghịch biến trên khoảng ( - ∞ ; - 2 )
B. Hàm f(x) đồng biến trên khoảng ( 1 ; + ∞ )
C. Trên (-1;1) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.
Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:
(I). Hàm số có tập xác định D=(-1;1).
(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.
(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.
(IV). Hàm số có một cực trị.
Số mệnh đề đúng là:
A.3
B.1
C.2
D.4