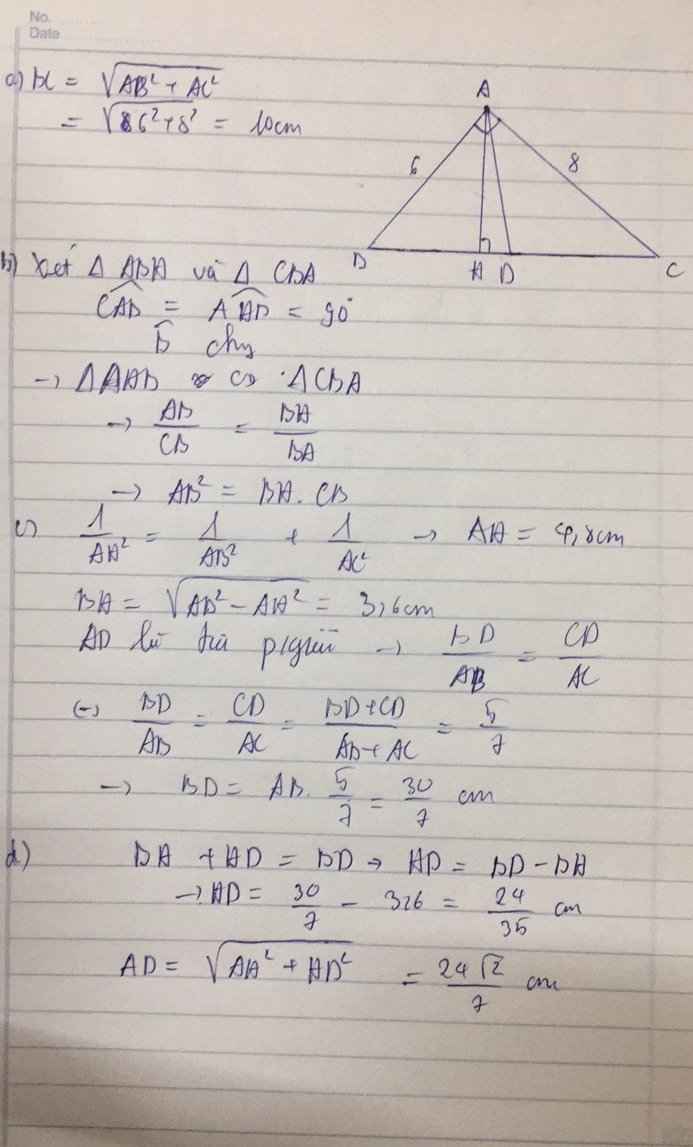tính giện tích hinh vẽ sau biet : AB= 8cm,BH=6cm

Những câu hỏi liên quan
tinh dien tich hinh ve sau biet : AC = 8cm BH=6cm
Hình nào hả bạn! Bạn phải thêm hình mới làm được chứ!
Đúng 0
Bình luận (0)
Mình dạy cho bạn cách vẽ nha!
B1: Bạn vào thanh công cụ của phần trả lời
B2: Bạn vào ô thứ tư (từ trái sang phải)
B3: Bạn vẽ hình vào trong đó
B4: Hoàn thành
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 2: Cho tam giác ABC vuông ở A, có AB 6cm; AC 8cm. Vẽ đường cao AH.a) Tính BC. b) Chứng minh AB2 BH.BC c) Tính BH; HC.Bài 3: Cho hình chữ nhật ABCD có AB 8cm, BC 6cm. Vẽ đường cao AH của tam giác ADB, (H BD) a) Chứng minh DAHB DBCD. b) Chứng minh AD2 HD.DB.c) Tính độ dài đoạn thẳng DH. cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
Đọc tiếp
Bài 2: Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a) Tính BC.
b) Chứng minh AB2 = BH.BC
c) Tính BH; HC.
Bài 3: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB, (H![]() BD)
BD)
a) Chứng minh DAHB ![]() DBCD.
DBCD.
b) Chứng minh AD2 = HD.DB.
c) Tính độ dài đoạn thẳng DH.
cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
thui hong cần nữa, hong cíu thì thui tui tự làm liu liu 
Đúng 1
Bình luận (5)
Cho tam giác ABC vuông A , có AB=6cm , AC=8cm . Vẽ đường cao AH.
a, Tính BC
b,CM: Tam giác ABC ~ Tam giác AHB
c,CM:\(AB^2=BH\cdot BC\).Tính BH,HC
d,Vẽ phân giác AD của góc A (D thuộc BC) Tính DB
\(a,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\left(pytago\right)\)
\(b,\) Vì \(\widehat{BAC}=\widehat{AHB}\left(=90\right);\widehat{ABC}.chung\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(c,\Delta ABC\sim\Delta HBA\left(cm.trên\right)\\ \Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\Rightarrow AB^2=BH\cdot BC\)
\(d,\) Vì AD là p/g góc A
\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\\ \Rightarrow DC=\dfrac{4}{3}BD\)
Mà \(BD+DC=BC=10\)
\(\Rightarrow\dfrac{4}{3}BD+BD=10\\ \Rightarrow\dfrac{7}{3}BD=10\\ \Rightarrow BD=\dfrac{30}{7}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a. Tính BC.
b. Chứng minh AB2 = BH.BC
c. Tính BH; HC.
a ΔABC vuông ở A
⇒Góc A= 90 độ
Áp dụng định lý Pitago vào ΔABC:
BC²=AB²+AC²
BC²=6²+8²
BC²=100
⇒BC=10 cm
b AB/HB=BC/BA
=> AB2=HB×BC
⇒HB=AB²/BC
⇒HB=6²/10=3,6(cm)
Tương tự: AC²=HC×BC
⇒HC=AC²/BC
⇒HC=8²/10=6,4(cm)
Vậy BH=3,6 cm và HC=6,4 cm
Đúng 4
Bình luận (1)
Cho tam giác ABC vuông tại A, có AB= 6cm; AC = 8cm, vẽ đường cao AH.
a, Tính AB
b, Chứng minh AB bình = BH nhân BC. Tính BH, HC
c, Vẽ phân giác AD của góc A(D thuộc BC). Chứng minh H nằm giữa B và D
a: Sửa đề: Tính BC
\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
b: ΔABC vuông tại A
mà AH là đường cao
nên AB^2=BH*BC
BH=6^2/10=3,6cm
CH=10-3,6=6,4cm
Đúng 0
Bình luận (0)
Cho ∆ABC vuông tại A có AB=6cm; AC=8cm. Vẽ đường cao AH. a) chứng minh ∆ABC đồng dạng ∆HBA. Tính BH? b) vẽ phân giác AD của ∆ABC. Tính HD?
a: Xét ΔABC và ΔHBA có
góc BAC=góc BHA
góc B chung
=>ΔABC đồng dạng với ΔHBA
BC=10cm
=>BH=6^2/10=3,6cm
b: \(AD=\dfrac{2\cdot6\cdot8}{6+8}\cdot cos45=\dfrac{24\sqrt{2}}{7}\left(cm\right)\)
AH=6*8/10=4,8cm
=>\(HD=\dfrac{24}{35}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tgiac ABC vuông tại A. Có AB= 6cm, AC=8cm. Vẽ đường cao AH.
a, Tính BC
b, Chứng minh AB2 = HB.BC
c, Tính BH, HC
giúp mình plssss :((
a, vì tam giác ABC vuông tại A , áp dụng định lí pytago ta có
\(AB^2+AC^2=BC^2=>BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10cm\)
b,xét tam giác ABH và tam giác CBA ta có
góc B chung
góc AHB= góc BAC=90 độ
=>tam giác ABH đồng dạng tam giác CBA(góc.góc)
=>\(\dfrac{BC}{AB}=\dfrac{AB}{BH}< =>AB^2=BH.BC\)
c,ta có \(AB^2=BH.BC=>BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=\dfrac{18}{5}cm\)
\(=>HC=BC-HB=10-\dfrac{18}{5}=\dfrac{32}{5}\)
Đúng 2
Bình luận (1)
Cho hình chữ nhật ABCD có AB 6cm, BC 8cm. Vẽ BH vuông góc với AC (H in AC )a) C/m: DeltaBHC sim DeltaCDAb) Tính diện tích DeltaBHCc) Gọi M, B lần lượt là trung điểm của AH và BH, tia MN cắt BC tại E. Chứng minh DeltaCEH sim DeltaCMB
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 6cm, BC = 8cm. Vẽ BH vuông góc với AC (H \(\in\) AC )
a) C/m: \(\Delta\)BHC \(\sim\) \(\Delta\)CDA
b) Tính diện tích \(\Delta\)BHC
c) Gọi M, B lần lượt là trung điểm của AH và BH, tia MN cắt BC tại E. Chứng minh \(\Delta\)CEH \(\sim\) \(\Delta\)CMB
Cho ABC vuông ở A, có AB = 6cm , AC = 8cm. Vẽ đường cao AH.
a) Tính BC b) Chứng minh ABC AHB
c) Chứng minh AB2 = BH.BC. Tính BH, HC
d) Vẽ phân giác AD của góc A ( D BC).Tính DB