Tiếp tuyến của đồ thị hàm số y = - x + 1 3 x - 2 tại giao điểm của đồ thị hàm số với trục tung có hệ số góc là:
A. -1
B. 1/4
C. -5/4
D. -1/4
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d : y = x - 2 2
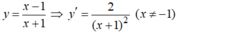
d: 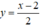 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi ( x 0 , y 0 ) là toạ độ của tiếp điểm.
- Ta có:
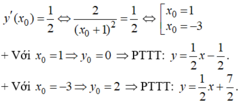
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)
Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)
\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)
Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2
(d1)//(d)
=>(d1): y=1/2x+b
=>y'=1/2
=>(x+1)^2=4
=>x=1 hoặc x=-3
Khi x=1 thì f(1)=0
y-f(1)=f'(1)(x-1)
=>y-0=1/2(x-1)=1/2x-1/2
Khi x=-3 thì f(-3)=(-4)/(-2)=2
y-f(-3)=f'(-3)(x+3)
=>y-2=1/2(x+3)
=>y=1/2x+3/2+2=1/2x+7/2
Hệ số góc của tiếp tuyến đồ thị hàm số y = x - 1 x + 1 tại giao điểm của đồ thị hàm số với trục tung bằng
A. -2
B. 1
C. 2
D. 1
Cho hàm số y = x + 2 x + 1 có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị (C) với trục tung là
A. y = x – 2
B. y = –x + 2
C. y = –x + 1
D. y = –x –2
Cho hàm số y=x lnx có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với đường thẳng d:x-1=0 là
A.x-y+1=0
B.x+y-1=0
C.x-y=0
D.x-y-1=0
Cho hàm số: y = – x 4 – x 2 + 6
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng: y = x/6 –1
a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10
a) Tính đạo hàm của hàm số \(y=\sqrt{sinx+cosx}\)
b) Hãy viết phương trình tiếp tuyến với đồ thị (C) của hàm số \(y=\dfrac{x+3}{x-1}\) biết tiếp tuyến vuông góc với đường thẳng \(y=\dfrac{1}{4}x+5\)
a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)
Cho hàm số y = x + 2 x + 1 C . Phương trình tiếp tuyến với đồ thị hàm số tại giao điểm của đồ thị (C) với trục tung là
A. y = − x + 2
B. y = − x + 1
C. y = x − 2
D. y = − x − 2
Đáp án A
Ta có y ' = − 1 x + 1 2 ; C ∩ O y = 0 ; 2 ⇒ y ' 0 = − 1
Do đó PTTT là: y = − x + 2
Cho hàm số y = x 2 + x + 1 x Hệ số góc k của tiếp tuyến của đồ thị hàm số y' tại điểm x=1 là
A. 3
B.2
C. 1
D. – 3