Cho hình lập phương A B C D . A ' B ' C ' D ' . Gọi M, N lần lượt là trung điểm của AD, BB'. Cosin của góc hợp bởi MN và AC' bằng
A. 2 3
B. 3 3
C. 5 3
D. 2 4
Cho hình lập phương A B C D . A ' B ' C ' D ' . Gọi M, N lần lượt là trung điểm của AD, BB'. Cosin của góc hợp bởi MN và AC' bằng
A. 2 3
B. 3 3
C. 5 3
D. 2 4
Gọi cạnh của hình lập phương là a.
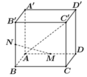
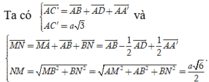
Suy ra
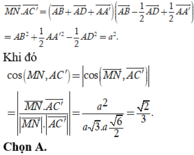
Cách 2. Gọi độ dài cạnh hình lập phương A B C D . A ' B ' C ' D ' là
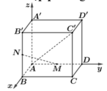
Chọn hệ trục tọa độ Oxyz sao cho ![]()
Khi đó, tọa độ các đỉnh:

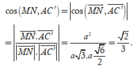
Cho hình lập phương ABCD.A 'B'C'D' có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A'C và MN.
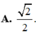
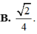
![]()
![]()
Cho hình chop S.ABCD có đáy là hình thoi cạnh a SO vuông góc với đáy ,SO= \(\frac{a\sqrt{6}}{3}\) OB=\(\frac{a\sqrt{3}}{3}\) Gộ M,N lần lượt là trung điểm SA và CD. Tính V SBMN theo a và tính góc giữa MN và (SBD)
Mn giúp mk giải đề này với.(Mn đừng bơ mk nha. Mơn mn nhìu)
1.Tìm tất cả các số tự nhiên có 3 chữ số abc trong hệ thập phân sao cho với n là số nguyên lớn hơn 2 ta có abc =\(n^2-1\)và cba =\(\left(n-2\right)^2\)
2.giải hpt:\(\hept{\begin{cases}x+y+\frac{1}{x}+\frac{2}{y}=5\\x^2+y^2+\frac{1}{x^2}+\frac{4}{y^2}=7\end{cases}}\)
3.a) Cho\(x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0\)và xy>0.Tìm max của M=\(\frac{1}{x}+\frac{1}{y}\)
b)CM:\(P=\frac{3-\sqrt{3+\sqrt{3+....+\sqrt{3}}}}{6-\sqrt{3+\sqrt{3+...+\sqrt{3}}}}< \frac{1}{5}\)(Tử có 2007 dấu căn,Mẫu có 2006 dấu căn)
4.Cho tam giác ABC nhọn nội tiếp đường tròn tâm O và có trực tâm H.Giả sử M là 1 điểm trên cung BC không chứa A
(M khác B,C).Gọi N,P lần lượt là điểm đối xứng của M qua các đường thẳng AB,AC.
a)CM: tứ giác AHCP nội tiếp
b)CM: N,H,P thẳng hàng
c)Tìm vị trí của M để NP lớn nhất
5. Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R). Gọi D,E,F, lần lượt là giao điểm của các đường thẳng AO vs BC;BO vs AC;CO vs AB.CM AD+BE+CF\(\ge\)\(\frac{9R}{2}\)
1. Cho hình lập phương ABCD.A'B'C'D' . Gọi M,N lần lượt là trung điểm cạnh A'B' và BC.
a) CMR \(MN\perp AC'\)
b) CMR: \(AC'\perp\left(A'BD\right)\)
2. Tìm a,b,c ∈ R để \(\lim\limits_{x\rightarrow1}\dfrac{2\sqrt{1+ax^2}-bx-1}{x^3-3x+2}=c\)
1.
\(\overrightarrow{MN}=\overrightarrow{MB'}+\overrightarrow{B'B}+\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{AB}-\overrightarrow{AA'}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{AC'}=\overrightarrow{AB'}+\overrightarrow{B'C'}=\overrightarrow{AB}+\overrightarrow{AA'}+\overrightarrow{AD}\)
\(\overrightarrow{MN}.\overrightarrow{AC'}=\left(\dfrac{1}{2}\overrightarrow{AB}-\overrightarrow{AA'}+\dfrac{1}{2}\overrightarrow{AD}\right)\left(\overrightarrow{AB}+\overrightarrow{AA'}+\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}AB^2-AA'^2+\dfrac{1}{2}AD^2=0\)
\(\Rightarrow MN\perp AC'\)
b.
\(\left\{{}\begin{matrix}AA'\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(ACC'A'\right)\Rightarrow BD\perp AC'\)
Tương tự: \(A'B\perp\left(ADC'B'\right)\Rightarrow A'B\perp AC'\)
\(\Rightarrow AC'\perp\left(A'BD\right)\)
2.
Phương trình \(x^3-3x+2=0\Leftrightarrow\left(x-1\right)^2\left(x+2\right)=0\) có nghiệm kép \(x=1\)
Nên giới hạn đã cho hữu hạn khi và chỉ khi phương trình: \(2\sqrt{1+ax^2}-bx-1=0\) có ít nhất 2 nghiệm \(x=1\) (tức là nghiệm bội 2 trở lên)
Thay \(x=1\) vào:
\(\Rightarrow2\sqrt{1+a}-b-1=0\Rightarrow2\sqrt{1+a}=b+1\)
\(\Rightarrow4\left(a+1\right)=b^2+2b+1\Rightarrow4a=b^2+2b-3\)
Khi đó:
\(\sqrt{4+4ax^2}-bx-1=0\Leftrightarrow\sqrt{4+\left(b^2+2b-3\right)x^2}-bx-1=0\)
\(\Leftrightarrow\sqrt{4+\left(b^2+2b-3\right)x^2}=bx+1\)
\(\Rightarrow4+\left(b^2+2b-3\right)x^2=b^2x^2+2bx+1\)
\(\Rightarrow\left(2b-3\right)x^2-2bx+3=0\)
\(\Rightarrow2bx^2-2bx-3x^2+3=0\)
\(\Rightarrow2bx\left(x-1\right)-\left(x-1\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2bx-3x-3\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\\left(2b-3\right)x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{2b-3}\end{matrix}\right.\) \(\Rightarrow\dfrac{3}{2b-3}=1\Rightarrow b=3\Rightarrow a=3\)
\(c=\lim\limits_{x\rightarrow1}\dfrac{2\sqrt{1+3x^2}-3x-1}{x^3-3x+2}=\dfrac{1}{8}\)
Cho tam giác ABC vuông tại A, trung tuyến AD, trọng tâm G
a,Cho biết \(\frac{AB}{AC}=\frac{3}{4}\)và AD=5 tính diện tích tam giác ABC
b, Qua G kẻ đường thẳng cắt AB, AC lần lượt tại M,N. Chứng minh rằng \(\frac{AB}{AM}+\frac{AC}{AN}=3\)
c,Kẻ các đường trung tuyến BE, CF của tam giác ABC Chứng minh rằng \(\sqrt{\frac{GA}{GD}}+\sqrt{\frac{GB}{GE}}+\sqrt{\frac{GC}{GF}}=\frac{3\sqrt{2}}{2}\)
Tính tổng sau:
\(A=\frac{1}{\left[\sqrt[3]{2}\right]}+\frac{1}{\left[\sqrt[3]{3}\right]}+\frac{1}{\left[\sqrt[3]{4}\right]}+\frac{1}{\left[\sqrt[3]{5}\right]}+\frac{1}{\left[\sqrt[3]{6}\right]}+\frac{1}{\left[\sqrt[3]{7}\right]}+\frac{1}{\left[\sqrt[3]{9}\right]}+...+\frac{1}{\left[\sqrt[3]{2012^3-1}\right]}\)
(trong tổng trên không có các số dạng \(\frac{1}{\left[\sqrt[3]{n}\right]}\) với n là lập phương 1 số nguyên,ví dụ:1 và 8)
Ta có từ n3 + 1 đến (n + 1)3 - 1 có
(n + 1)3 - 1 - n3 - 1 + 1 = 3n2 + 3n số có phần nguyên bằng n
Áp dụng vào cái ban đầu ta có
\(=\frac{3.1^2+3.1}{1}+\frac{3.2^2+3.2}{2}+...+\frac{3.2011^2+3.2011}{2011}\)
= 3.1 + 3 + 3.2 + 3 + ...+ 3.2011 + 3
= 3.2011 + 3(1 + 2 +...+ 2011)
= 6075231
Biết rằng a là số tự nhiên không chính phương thì \(\sqrt{a}\)là số vô tỉ
Gỉai thích các tập hơp sau tập hợp nào là số hữu tỉ tập hợp nào không phải:
\(\frac{3}{\sqrt{7}-5}-\frac{3}{\sqrt{7}+5}\)
\(\frac{4}{2-\sqrt{3}}-\frac{4}{2+\sqrt{3}}\)
\(\frac{\sqrt{3}}{\sqrt{7}-2}-2\sqrt{7}\)
\(\frac{\sqrt{7}+5}{\sqrt{7}-5}+\frac{\sqrt{7}-5}{\sqrt{7}+5}\)
Thế muốn giải thích thì liệt kê đau đầu =(
\(\frac{3}{\sqrt{7}-5}-\frac{3}{\sqrt{7+5}}=\frac{-10}{9}\inℚ\)
\(\frac{\sqrt{7}+5}{\sqrt{7}-5}+\frac{\sqrt{7}-5}{\sqrt{7}+5}=12\inℚ\)
Đây là TH là số hữu tỉ còn lại.....
\(\frac{4}{2-\sqrt{3}}-\frac{4}{2+\sqrt{3}}=8\sqrt{3}\notinℚ\)
\(\frac{\sqrt{3}}{\sqrt{7}-2}-2\sqrt{7}=2-\sqrt{7}\notinℚ\)
Thử sức đề mình soạn cho các bạn có mục tiêu thi HSG toán 9 ( học kỳ I ) thôi nhé :D
Câu 1:
a) Tính giá trị biểu thức \(E=\frac{\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}}{\sqrt[3]{\sqrt[3]{2}-1}}\)
b) Cho x,y thỏa mãn \(x\ne\pm y\) Đặt \(\frac{x+y}{x-y}+\frac{x-y}{x+y}=a\)
Tính giá trị của biểu thức \(M=\frac{x^4+y^4}{x^4-y^4}+\frac{x^4-y^4}{x^4+y^4}\)
Câu 2:
a) Giải phương trình: \(\frac{\sqrt{3x+1}+\sqrt{x+3}}{x+5+\sqrt{2\left(x^2+1\right)}}=\left(1-x\right)\sqrt{1-x}+\frac{3-3\sqrt{x}}{2}\)
b) Giải hệ phương trình: \(\hept{\begin{cases}14x^2-21y^2-6x+45y-14=0\\35x^2+28y^2+41x-122y+56=0\end{cases}}\)
Câu 3:
a) Cho \(x_0;x_1;x_2;.......\) được xác định bởi: \(x_n=\left[\frac{n+1}{\sqrt{2}}\right]-\left[\frac{n}{\sqrt{2}}\right]\).
Hỏi trong 2006 số đầu tiên của dãy có mấy số khác 0
b) Giải phương trình nghiệm nguyên: \(m^n=n^{m-n}\)
c) Cho phương trình \(x^2-4x+1=0\). Gọi \(x_1;x_2\) là 2 nghiệm của phương trình. Đặt \(a_n=\frac{x_1^n+x_2^n}{2\sqrt{3}}\) với n là số nguyên dương. Chứng minh rằng \(a_n\) là một số nguyên với mọi n
d) Cho bộ số nguyên dương thỏa mãn \(a^2+b^2=c^2\). Chứng minh rằng không thể tồn tại số nguyên dương n sao cho:
\(\left(\frac{c}{a}+\frac{c}{b}\right)^2=n\)
Câu 4:
a) Cho các số dương a,b,c. Chứng minh rằng:
\(\frac{a\left(b+c\right)}{a^2+bc}+\frac{b\left(c+a\right)}{b^2+ca}+\frac{c\left(a+b\right)}{c^2+ab}\ge1+\frac{16abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
b) Cho các số không âm a,b,c thỏa mãn \(\left(a+b\right)\left(b+c\right)\left(c+a\right)>0\)Tìm giá trị nhỏ nhất của biểu thức:
\(A=\sqrt{\frac{b^2-bc+c^2}{a^2+bc}}+\sqrt{\frac{c^2-ca+a^2}{b^2+ca}}+\sqrt{\frac{a^2-ab+b^2}{c^2+ab}}+\frac{2\left(ab+bc+ca\right)}{a^2+b^2+c^2}\)
Câu 5:
1)
Cho tam giác ABC có 3 đường cao AD, BE, CF cắt nhau tại H, EF cắt BC tại P. Qua D kẻ đường thẳng song song EF cắt AB, AC lần lượt tại Q, R.
a) Chứng minh rằng \(\frac{PB}{PC}=\frac{DB}{DC}\)
b) Gọi X là trung điểm AH. EF cắt AH tại Y. Chứng minh rằng Y là trực tâm tam giác XBC.
2)
Cho E và F lần lượt là các trung điểm của cạnh AD và CD của hình bình hành ABCD sao cho \(\widehat{AEB}=\widehat{AFB}=90^0\), và G là điểm nằm trên BF sao cho EG // AB. Gọi DH, AF lần lượt cắt cạnh BC, BE tại I, H. Chứng minh rằng \(FI\perp FH\)
Câu 6:
Tìm giá trị nhỏ nhất của a là cạnh hình vuông sao cho có thể đặt 5 tấm bìa hình tròn bán kính 1 trong hình vuông đó mà các tấm bìa không chờm lên nhau.
GOODLUCK.
WARNING: COMMENT LUNG TUNG SẼ BỊ CÔ QUẢN LÝ CHO "PAY ẶC" nhé !
Thời gian làm bài ( 180 phút ).
Thời gian được tính từ 7 giờ 30 phút từ sáng mai nha mọi người :D ai làm được bài nào ( 1 ý thôi cũng được ) thì " chốt đơn" 11h post lên nhé :D
Bất đẳng thức học kì mà cho vậy có lẽ không phù hợp á bác Cool Kid.
4a) Xét hiệu 2 vế ta được:
\(\frac{\Pi\left(a+b\right)\left[\Sigma a\left(b-c\right)\right]^2+\left[3\Sigma a\left(b^2+c^2\right)+22abc\right]\Pi\left(a-b\right)^2}{4\left(a+b\right)\left(b+c\right)\left(c+a\right)\left(a^2+bc\right)\left(b^2+ca\right)\left(c^2+ab\right)}\ge0\)
Đề hơi dễ nhỉ bác :3
cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi O là tâm ABCD; M,N lần lượt là trung điểm AB,AD.
1. BD vuông góc (ACC'A') và A'C vuông góc(BDC'), A'C vuông góc AB', (BDC') vuông góc(ACC'A') và (MNC) vương góc (ACC'A')
2. Tính d(C,(BDC')),d(C,(MNC'))
3. Tính tan(AC,(MNC')) và tan((BDC'),(ABCD))
4. Tính cosin((MNC'),(BDC'))
5. Tính d(AB',BC')