Cho tổng M = C 2018 0 3 2018 + C 2018 1 3 2017 2 + C 2018 2 3 2016 2 2 + ... + C 2018 2018 2 2018 . Khi viết M dưới dạng một số trong hệ thập phân thì số này có bao nhiêu chữ số?
A. 1410
B. 1412
C. 1413
D. 1411
cho a,b,c#0 và a+b+c#0 thõa mãn 1/a+1/b+1/c=1/a+b+c
chứng minh: 1/a^2018+1/b^2018+1/c^2018=1/a^2018+b^2018+c^2018
Cho a+b = 0 và a*b+ a*c+b*c=0 Tính giá trị của biểu thức M = (a -2018)^2018+(b-2017)^2018-(c+2017)^2018
Cho các sô nguyên a,b,c,d khác 0 thỏa mãn ab=cd.Cmr a^2018+b^2018+c^2018+d^2018 là hợp số
Cho a+b+c=0 và ab+bc+ac=0. Tính giá trị của biểu thứa: M= (a-2018)^2014 + ( b-2018)^2014 - (c+2018)^2014
\(a+b+c=0\)
\(\Leftrightarrow\left(a+b+c\right)^2=0\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=0\)
\(\Leftrightarrow a^2+b^2+c^2=0\)
Mà \(a^2;b^2;c^2\ge0\forall a;b;c\) nên điều này xảy ra \(\Leftrightarrow a=b=c=0\)
\(\Rightarrow M=2018^{2014}+2018^{2014}-2018^{2014}=2018^{2014}\)
Cho hai tổng: A = 1+2+3+...+2018
B = 1+2+3+...+2018+2019
Trong hai tổng trên có thể thay một số dấu + bằng dấu - để A=0 hoặc B = 0 được hay không, vì sao
Cho 3 số thực a,b,c khác 0 thỏa mãn a+b+c=1 và 1/a+1/b+1/c=1.Tính giá trị biểu thức P=a2018+b2018+c2018
Cho a,b,c >0 thỏa mãn a+b+c=2018
C/m A=\(\frac{a}{2018-c}+\frac{b}{2018-a}\) +\(\frac{c}{2018-b}\) không thuộc Z
A=a/2018-c +b/2018-a +c/2018-b
A= a/a+b + b/b+c + c/c+a
Nhận thấy: a/a+b< a/a+b+c; b/b+c<b/a+b+c; c/c+a<c/a+b+c
Do đó A= a/a+b + b/b+c + c/c+a < a/a+b+c + b/a+b+c + c/a+b+c = a+b+c/a+b+c=1
=>A>1(1)
áp dụng t/c:a/b<1=>a/b<a+n/b+n(a,b,n khác 0), ta có:
a/a+b < a+c/a+b+c ; b/b+c < b+a/b+c+a ; c/c+a < c+b/c+a+b
Do đó :A= a/a+b + b/b+c + c/c+a < a+c/a+b+c + b+a/a+b+c + c+b/a+b+c= 2(a+b+c)/a+b+c=2
=>A<2(2)
từ (1);(2)=>1<A<2=> A không thuộc Z=>ĐPCM. chúc bạn học tốt
cho a+b+c = a3+b3+c3=1
tính M = a2018+b2018+c2018
Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
![]()
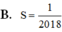
![]()
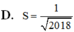
cho A+B+C=0 và AB+AC+BC=0
TÍNH M=\(\left(A-2018\right)^{2019}+\left(B-2018\right)^{2019}-\left(C+2018\right)^{2019}\)
Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac\)
\(\Rightarrow a^2+b^2+c^2=\left(a+b+c\right)^2-2\left(ab+bc+ac\right)\)
hay \(a^2+b^2+c^2=0\Rightarrow a=b=c=0\)
Thay a = b = c = 0 vào M rồi tính như bình thường nha bạn!
Ta có :
\(a+b+c=0\)
\(\Leftrightarrow\)\(\left(a+b+c\right)^2=0\)
\(\Leftrightarrow\)\(a^2+b^2+c^2+2ab+2bc+2ca=0\)
\(\Leftrightarrow\)\(a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\)
\(\Leftrightarrow\)\(a^2+b^2+c^2=0\)
\(\Leftrightarrow\)\(\hept{\begin{cases}a^2=0\\b^2=0\\c^2=0\end{cases}\Leftrightarrow a=b=c=0}\)
\(\Rightarrow\)\(M=\left(a-2018\right)^{2019}+\left(b-2018\right)^{2019}-\left(c+2018\right)^{2019}\)
\(\Rightarrow\)\(M=-2018^{2019}-2018^{2019}-2018^{2019}\)
\(\Rightarrow\)\(M=-3.2018^{2019}\)
Chúc bạn học tốt ~